今回のテーマは【ヤング係数】
定義や計算(単位)の求め方のほか、コンクリートや木材など、材料別にヤング係数一覧表もありますので合わせてご確認ください。
それではさっそく参りましょう、ラインナップは目次からどうぞ 🙂
ヤング係数の求め方とは?計算の公式や一覧(コンクリートや木材も)
ヤング係数とは、材料(材質)の硬さを表す指標です。
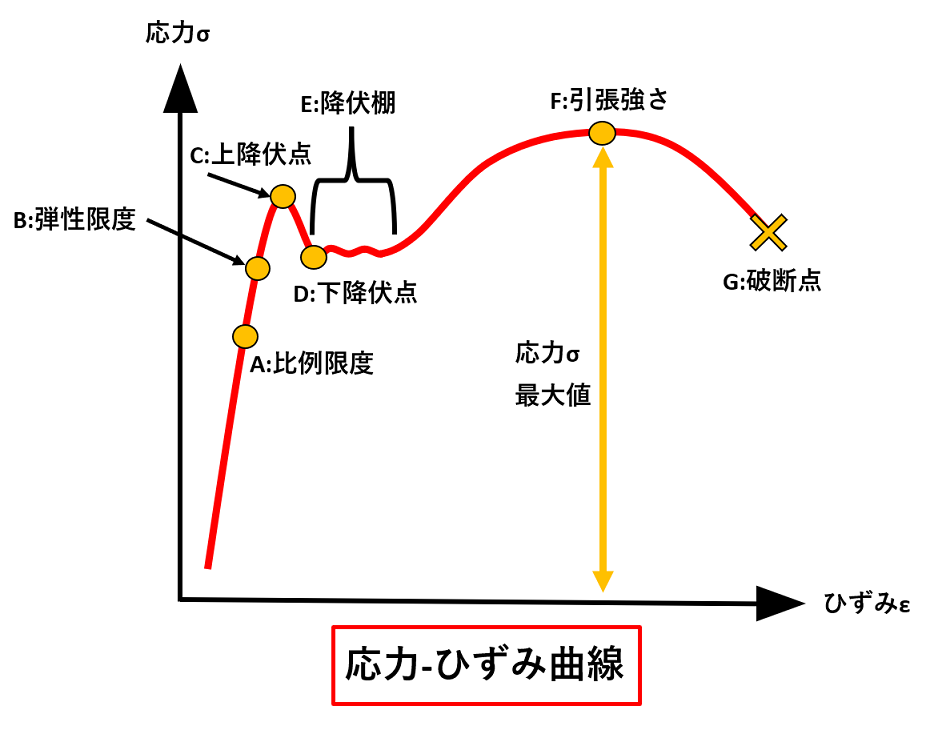
応力とひずみが関係しており、求め方は以下の公式を使います。(応力-ひずみ曲線の勾配がヤング係数)
ヤング係数E=応力σ(N)/ひずみε(mm²)
よってヤング係数の単位はN/mm²で表すことができますね 🙂
応力-ひずみ曲線についても意味や語句を確認しておくと良いでしょう。
またここでひとつ、ヤング係数の単位変換を実際に計算してみましょう。
たとえば、鋼のヤング係数をMPaからN/m㎡に変換してみると、
205000 MPa ⇒ 205000 N/m㎡
次に鋼のヤング係数をMPaからGpaに変換してみると、
205000 MPa ⇒ 205 Gpa
となります。

ヤング係数の材料別一覧!計算公式も
ヤング係数は材料によって値が異なります。
材料一覧
- 鋼材
- コンクリート
- 木材
- アルミ
- ステンレス
- ガラス
- プラスチック

鋼材のヤング係数

一般的な鋼材のヤング係数は20.5×10⁴N/mm²(205GPa)です。
鋼材は強度も強く、使い勝手が良いため、建設資材などに多用されています。
コンクリートのヤング係数

コンクリートの応力ひずみ曲線は、鋼材のような直線とはならず、コンクリートに生じる応力度が大きくなるほど緩やかな曲線を示します。
つまりコンクリートのヤング係数は、その圧縮強度が高いほど大きな値となります。
一方で、コンクリートに生じる応力度が大きくなるほど、ヤング係数は小さくなることが分かるでしょう。
そしてヤング係数は
Ec=3.35 × 104 × ( γ / 24 )2 × ( Fc / 60 )1/3
の式から導くことができます。
Ec=鉄筋コンクリートのヤング係数
γ=コンクリートの単位体積重量
Fc=コンクリートの設計基準強度
ちなみに普通コンクリートで、γ=23、Fc=24のヤング係数は以下のとおりです。
Ec=3.35 × 104 × ( 23 / 24 )2 × ( 24 / 60 )1/3=2.26×10⁴N/mm²
木材のヤング係数
一般的は木材のヤング係数は7000~12000N/mm²程度。
ただし木材は、スギやヒノキなど種類によって強度もヤング係数も違います。
木材の種類によって、強度の確認が必要になるので注意しましょう。
木材の種類別のくわしいヤング係数が知りたい方は別記事でまとめていますのでぜひどうぞ!
アルミのヤング係数
アルミは強度がいくら高くても、ヤング係数は一定です。
7000N/mm²で、鋼の1/3程度と覚えておくと良いでしょう。
ステンレスのヤング係数
ステンレス鋼(SUS304A)のヤング係数は1.93×105N/mm²です。
ただし全鋼種について一般鋼より低く(または同等)、変形が大きくなりますのでご注意下さい。
| 鋼種の機械的性質 | マルテンサイト系 (13Cr系) SUS410 | フェライト系 (18Cr系) SUS430 | オーステナイト系 (18Cr-8Ni系) SUS304 | 炭素鋼 SN400 |
|---|---|---|---|---|
| 弾性係数(kN/mm2) | 205 | 193 | 200 | 200 |
| 耐力(降伏点)(N/mm2) | 275 | 305 | 255 | 275 |
| 引張強さ(N/mm2) | 510 | 550 | 590 | 430 |
| 降伏比 | 0.53 | 0.55 | 0.43 | 0.64 |
| 伸び(%) | 25 | 27 | 60 | 28 |
マルテンサイト系は焼き入れ前の焼鈍材ではフェライト組織になっているため機械的性質はフェライト系とほぼ同じ。
フェライト系とオーステナイト系で比べると、オーステナイト系は引張強さが大きく加工による硬化が大きく伸びも大きいのが特徴です。
ガラスのヤング係数

板ガラスのヤング係数(ヤング率)は、一般的に7.16×10⁴N/mm²です。
ただし、ガラスにもいくつか種類があり、強化ガラスなどはヤング係数も高くなる傾向にあります。
ガラスの種類などについてさらにくわしく知りたい方は別記事でご確認ください。
プラスチックのヤング係数
家電などに使われる身近なプラスチック(ABSやPPなど)はのヤング係数は1,000~2500N/mm²程度です。
ちなみに同じ形状のものであれば、同じ長さだけ変化させるのに、プラスチックは金属の1/10~1/100の力で変形させることができます。
変形しやすいことにはメリットもデメリットもあるので、プラスチックの特性をよく理解して使用することが大切ですね。
銅のヤング係数
銅のヤング係数は129.8GPa(129,800N/mm²)
やはり金属系は硬いため、応力に対する抵抗力も高くなり、それに伴ってヤング係数も大きくなります。
ヤング係数と関係する計算の求め方や公式(断面二次モーメント・せん断力・変形・たわみ)
変形量は、ヤング係数Eと断面二次モーメントIに反比例します。
EとIが大きければ、変形量は小さくなるということです。
ちなみに鋼よりもコンクリートの方が、ヤング係数Eが小さいので変形量が大きくなります。
また、構造力学の公式としては以下も覚えておくと良いでしょう。
ヤング係数との、たわみ、変形、せん断力、モーメントの関係が分かります。
| 荷重の状態
単純ばり |
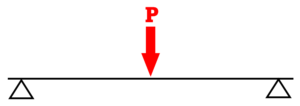
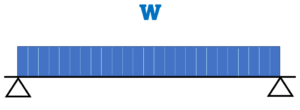
集中荷重P | 等分布荷重w |
| 端部曲げモーメント | M=0 | M=0 |
| 中央部曲げモーメント | M=P×(L/4) | M=w×(L²/8) |
| せん断力 | Q=P/2 | Q=w×L/2 |
| 変形 | δ=PL³/48EI | δ=5wL⁴/384EI |
| たわみ | θ=PL²/16EI | θ=wL³/24EI |
| 荷重の状態
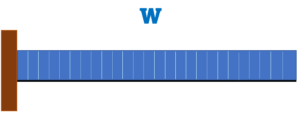
片持ちばり |
集中荷重P | 等分布荷重w |
| 端部曲げモーメント | M=P×L | M=w×(L²/2) |
| 中央部曲げモーメント | ― | ― |
| せん断力 | Q=P | Q=w×L |
| 変形 | δ=PL³/3EI | δ=wL⁴/8EI |
| たわみ | θ=PL²/2EI | θ=wL³/6EI |
| 荷重の状態
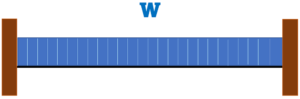
両端固定ばり |
集中荷重P | 等分布荷重w |
| 端部曲げモーメント | M=P×(L/8) | M=w×(L²/12) |
| 中央部曲げモーメント | M=P×(L/8) | M=w×(L²/12) |
| せん断力 | Q=P/2 | Q=w×L/2 |
| 変形 | δ=PL³/192EI | δ=wL⁴/384EI |
| たわみ | θ=0 | θ=0 |
さらにくわしく知りたい方は構造力学の基礎公式集をご確認ください。
ヤング係数の求め方とは?計算の公式や一覧(コンクリートや木材も)まとめ
ヤング係数とは、材料(材質)の硬さを表す指標
ヤング係数E=応力σ(N)/ひずみε(mm²)
ヤング係数が大きい順にまとめてみるとこんな感じ 🙂
| ヤング係数 | 材料一覧 | ヤング係数 |
|
大きい ↑ ↓ 小さい |
鋼材 | 205GPa(205,000N/mm²) |
| 銅 | 129.8GPa(129,800N/mm²) | |
| ガラス | 7.16×10⁴N/mm²(板ガラス) | |
| コンクリート | Ec=3.35 × 10⁴ × ( γ / 24 )² × ( Fc / 60 )^(1/3)
普通コンクリート2.26×10⁴N/mm²(γ = 23、Fc = 24) |
|
| ステンレス | 1.93×105N/mm2(ステンレス鋼(SUS304A)) | |
| 木材 | 7000~12000N/mm² | |
| アルミ | 7000N/mm² | |
| プラスチック | 1,000~2500N/mm²(ABSやPPなど) |
参考にしてください。
以上です。
ありがとうございました。