土木・建築のテストや建設業の現場でも使える構造力学公式一覧が見たい！
よく使う構造力学の基礎公式を一覧にまとめましたので、ぜひ参考にしてください。
それではさっそくまいりましょう、ラインナップは目次で確認してください。
構造力学の公式一覧！ひずみや応力・はりのたわみ公式集
構造力学の公式をチェックしていきましょう。
構造力学の公式一覧➀応力の基礎公式
垂直応力
垂直応力とは、その名のとおり、垂直方向に作用する力のことです。
垂直応力σ＝P／A［N/㎡］
σ：垂直応力、P：外力［Ｎ］、A：断面積［㎡］
せん断応力
せん断応力とは、物体内部のある面と平行方向に、その面にすべらせるように作用する力のことです。
力がずれるようなイメージをもっておくと良いでしょう。
せん断応力τ＝P／A［N/㎡】
τ：せん断応力、P：外力［Ｎ］、A：断面積［㎡］
構造力学の公式一覧②ひずみの基礎公式
ひずみとは、物体に外力を加えたときに現れる、形や体積の変化のことです。
ひずみε＝δ／ｌ
ε：ひずみ、δ：伸び（縮み）［ｍ］、ｌ：初期長さ［ｍ］
構造力学の公式一覧③フックの法則
フックの法則とは、ばねの伸びは引く力に比例するという法則です。
フックの法則σ＝Eε
E：弾性係数（ヤング率）、ε：ひずみ
断面二次モーメントImm⁴と断面係数Zmm³の基礎公式
| 図形 | 断面二次モーメントI［ｍｍ⁴］ | 断面形数Z［ｍｍ³］ |
| 正方形☐ | I＝ｈ⁴／１２ ［ｈ＝高さ］ | Z＝ｈ³／６ ［ｈ＝高さ］ |
| 長方形▭ | I＝ｂｈ³／１２［ｂ＝底（上）辺,ｈ＝高さ］ | Z＝ｂｈ²／６ ［ｂ＝底（上）辺,ｈ＝高さ］ |
| 三角△ | I＝ｂｈ³／３６［ｂ＝底辺,ｈ＝高さ］ | Z＝ｂｈ²／２４［ｂ＝底辺,ｈ＝高さ］ |
| 円形〇 | I＝πD⁴／６４ ［D＝直径］ | Z＝πD³／３２ ［D＝直径］ |
断面二次モーメントは、材料の曲げにくさ（曲げる力に対する抵抗性）、断面係数は、部材の断面性能を表す値のこと！曲げる力（曲げモーメント）に対する強さ・抵抗力とも表せるね☆
モーメントについて詳しく知りたいかたは、また別記事でまとめていますのでご確認ください。
構造力学のはりのたわみ基礎公式一覧
はりについては、
- 単純ばり
- 片持ちばり
- 両端固定ばり
の３つの基本ばりの公式をご紹介します。
構造力学➀単純ばり＆たわみ基礎公式
| 荷重の状態 | 集中荷重P |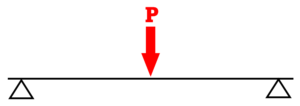
等分布荷重ｗ
|
| 端部曲げモーメント | M＝０ | M＝０ |
| 中央部曲げモーメント | M＝P×（L／４） | M＝ｗ×（Ｌ²／８） |
| せん断力 | Ｑ＝Ｐ／２ | Ｑ＝ｗ×Ｌ／２ |
| 変形 | δ＝ＰＬ³／４８ＥＩ | δ＝５ｗＬ⁴／３８４ＥＩ |
| たわみ | θ＝ＰＬ²／１６ＥＩ | θ＝ｗＬ³／２４ＥＩ |
- M：曲げモーメント
- P：集中荷重（外力）
- Q：せん断力
- ｗ：等分布荷重
- δ：伸び（縮み）
- Ｌ：はりの長さ
- Ｅ：弾性係数（ヤング率）
- Ｉ：弾性二次モーメント
構造力学②片持ちばり＆たわみ基礎公式
| 荷重の状態 | 集中荷重P
|
等分布荷重ｗ
|
| 端部曲げモーメント | M＝Ｐ×Ｌ | M＝ｗ×（Ｌ²／２） |
| 中央部曲げモーメント | ― | ― |
| せん断力 | Ｑ＝Ｐ | Ｑ＝ｗ×Ｌ |
| 変形 | δ＝ＰＬ³／３ＥＩ | δ＝ｗＬ⁴／８ＥＩ |
| たわみ | θ＝ＰＬ²／２ＥＩ | θ＝ｗＬ³／６ＥＩ |
- M：曲げモーメント
- P：集中荷重（外力）
- Q：せん断力
- ｗ：等分布荷重
- δ：伸び（縮み）
- Ｌ：はりの長さ
- Ｅ：弾性係数（ヤング率）
- Ｉ：弾性二次モーメント
構造力学③両端固定ばり＆たわみ基礎公式
| 荷重の状態 | 集中荷重P
|
等分布荷重ｗ
|
| 端部曲げモーメント | M＝Ｐ×（Ｌ／８） | M＝ｗ×（Ｌ²／１２） |
| 中央部曲げモーメント | M＝Ｐ×（Ｌ／８） | M＝ｗ×（Ｌ²／１２） |
| せん断力 | Ｑ＝Ｐ／２ | Ｑ＝ｗ×Ｌ／２ |
| 変形 | δ＝ＰＬ³／１９２ＥＩ | δ＝ｗＬ⁴／３８４ＥＩ |
| たわみ | θ＝０ | θ＝０ |
- M：曲げモーメント
- P：集中荷重（外力）
- Q：せん断力
- ｗ：等分布荷重
- δ：伸び（縮み）
- Ｌ：はりの長さ
- Ｅ：弾性係数（ヤング率）
- Ｉ：弾性二次モーメント
はりの問題についてはまた別記事でまとめていますのでぜひチェックしてみてください。
構造力学の公式一覧！ひずみや応力・はりのたわみ公式集まとめ
構造力学基礎公式一覧表！
構造力学公式まとめ
垂直応力σ＝P／A［N/㎡］ σ：垂直応力、P：外力［Ｎ］、A：断面積［㎡］
せん断応力τ＝P／A［N/㎡］ τ：せん断応力、P：外力［Ｎ］、A：断面積［㎡］
ひずみε＝δ／ｌ ε：ひずみ、δ：伸び（縮み）［ｍ］、ｌ：初期長さ［ｍ］
フックの法則σ＝Eε E：弾性係数（ヤング率）、ε：ひずみ
断面二次モーメントと断面係数
| 正方形☐ | I＝ｈ⁴／１２ ［ｈ＝高さ］ | Z＝ｈ³／６ ［ｈ＝高さ］ |
| 長方形▭ | I＝ｂｈ³／１２［ｂ＝底（上）辺,ｈ＝高さ］ | Z＝ｂｈ³／６ ［ｂ＝底（上）辺,ｈ＝高さ］ |
| 三角△ | I＝ｂｈ³／３６［ｂ＝底辺,ｈ＝高さ］ | Z＝ｂｈ²／２４［ｂ＝底辺,ｈ＝高さ］ |
| 円形〇 | I＝πD⁴／６４ ［D＝直径］ | Z＝πD³／３２ ［D＝直径］ |
はりのたわみ
| 荷重の状態
単純ばり |
集中荷重P
|
等分布荷重ｗ
|
| 端部曲げモーメント | M＝０ | M＝０ |
| 中央部曲げモーメント | M＝P×（L／４） | M＝ｗ×（Ｌ²／８） |
| せん断力 | Ｑ＝Ｐ／２ | Ｑ＝ｗ×Ｌ／２ |
| 変形 | δ＝ＰＬ³／４８ＥＩ | δ＝５ｗＬ⁴／３８４ＥＩ |
| たわみ | θ＝ＰＬ²／１６ＥＩ | θ＝ｗＬ³／２４ＥＩ |
| 荷重の状態
片持ちばり |
集中荷重P
|
等分布荷重ｗ
|
| 端部曲げモーメント | M＝Ｐ×Ｌ | M＝ｗ×（Ｌ²／２） |
| 中央部曲げモーメント | ― | ― |
| せん断力 | Ｑ＝Ｐ | Ｑ＝ｗ×Ｌ |
| 変形 | δ＝ＰＬ³／３ＥＩ | δ＝ｗＬ⁴／８ＥＩ |
| たわみ | θ＝ＰＬ²／２ＥＩ | θ＝ｗＬ³／６ＥＩ |
| 荷重の状態
両端固定ばり |
集中荷重P
|
等分布荷重ｗ
|
| 端部曲げモーメント | M＝Ｐ×（Ｌ／８） | M＝ｗ×（Ｌ²／１２） |
| 中央部曲げモーメント | M＝Ｐ×（Ｌ／８） | M＝ｗ×（Ｌ²／１２） |
| せん断力 | Ｑ＝Ｐ／２ | Ｑ＝ｗ×Ｌ／２ |
| 変形 | δ＝ＰＬ³／１９２ＥＩ | δ＝ｗＬ⁴／３８４ＥＩ |
| たわみ | θ＝０ | θ＝０ |
今回は以上です。
参考になればうれしいです。
ありがとうございました。