物理や力学では必須となる物体の【重心】
重心とは、物体に働く重力の合力の作用点のこと。
正方形であればど真ん中だし、三角形だと重心は下の方(広がりが大きい方)にズレます。
だけど単純な形の物体ばかりではないですよね。
だから今回は、図心と重心の違いや、いろんな物体の重心の求め方について解説していきますよー!
それではさっそく参りましょう、ラインナップは目次からどうぞ 😀
図心と重心の違い!重心の求め方も簡単にわかりやすく解説
ズバリ重心と図心のちがいは、重さを考慮しているかどうかということ!
たとえば、同じ材質で作られた正方形や三角形などの物体は、【重心=図心】となります。
しかしながら、材質が異なる物体、たとえば円の半分が鉄、半分が木でできていた場合、図心は円の中心ですが、重心は鉄(重い)のほうにズレます。
違いはこんな感じなので、豆知識として覚えておくと良いでしょう。
はい、というわけで、さっそく重心の求め方についてやっていきましょう。
やり方としては2通り解説していきます。
重心の求め方
- 不定形の物体の重心の求め方
- 物体形の重心の求め方
不定形の物体の重心の求め方
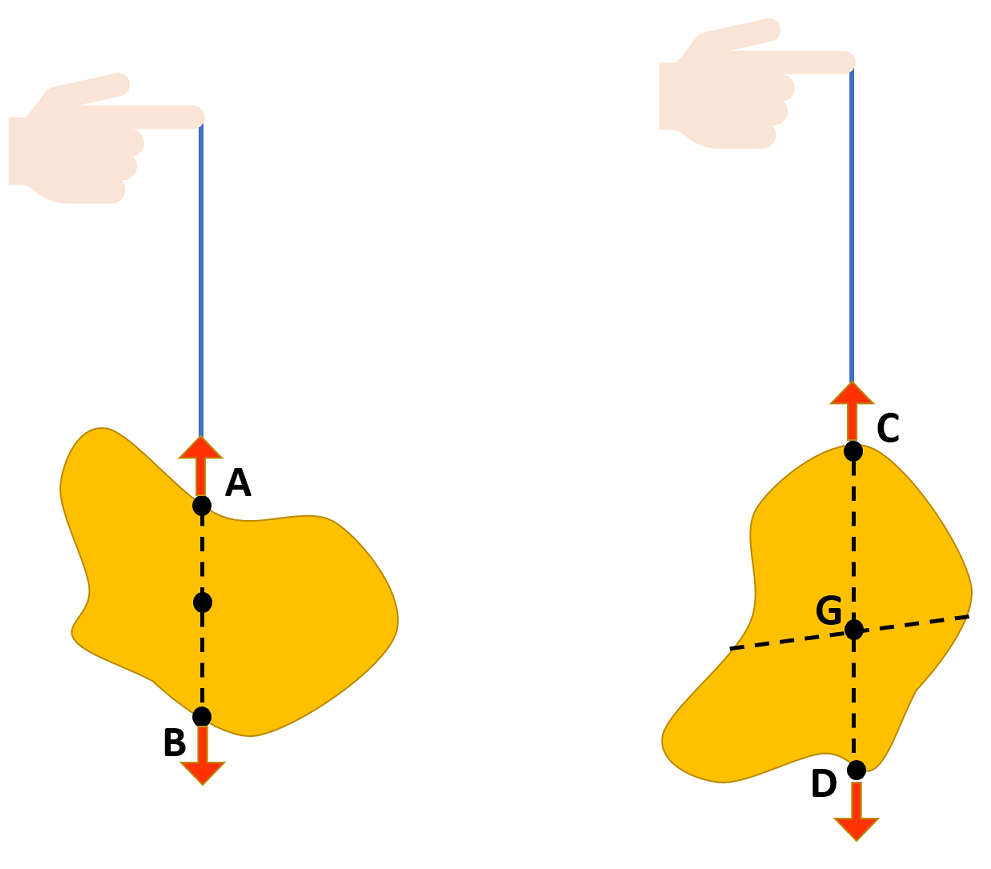
不定形の物体における重心を求めるには、物体を糸で吊るしてみると分かります。(上記図解参照)
2箇所ほど選んで不定形の物体を糸で吊るしてみると、糸の張力Fと重力Wは同一作用線上にあるため、重心GはAB上のどこかにあることが分かります。
そして別の点Cに糸をつけて物体を吊るすと、この場合も重心はCを通る鉛直線CD上のどこかにあるはずであるから、直線CDを板の上に書くと、重心はAB、CDの交点として求めることができるわけです。
物体形の重心の求め方
つづいては、重心をxy座標で考えていきましょう。
たとえば、質量m₁、m₂、m₃の3枚板が並べられていて、各板の重心G₁、G₂、G₃の座標が与えられているとき、この物体の全体の重心Gを求めてみます。
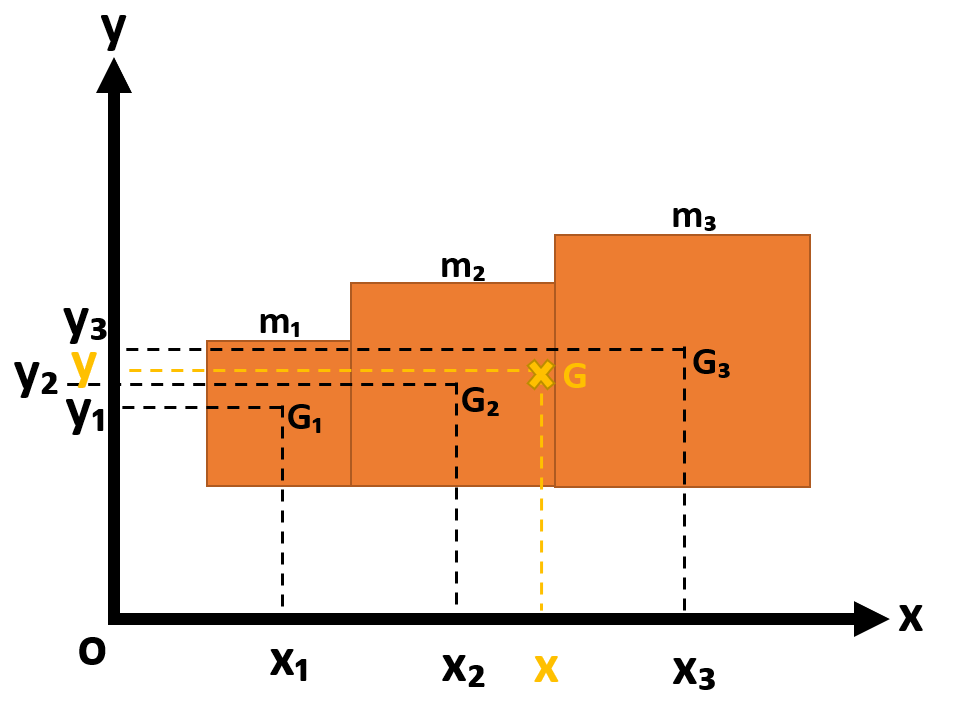
原点に関する重力のモーメントを考えると、各板の重心に働く重力モーメントの和は、全体の重心に働く重力のモーメントに等しいです。
したがって、重力が-y方向に働いているとき、
-m₁gx₁-m₂gx₂-m₃gx₃=-(m₁+m₂+m₃)gx
よってx=(m₁x₁+m₂x₂+m₃x₃)/(m₁+m₂+m₃)
同様に重力が-x方向に働いているとき、
y=(m₁y₁+m₂y₂+m₃y₃)/(m₁+m₂+m₃)
となります。
つまり、物体系の重心のx(y)座標は、各物体の質量と重心のx(y)座標との積の和を全体の質量で割れば求めることができます。
ここでひとつ、例題を解いてみましょう。

【例題(重心の位置)】
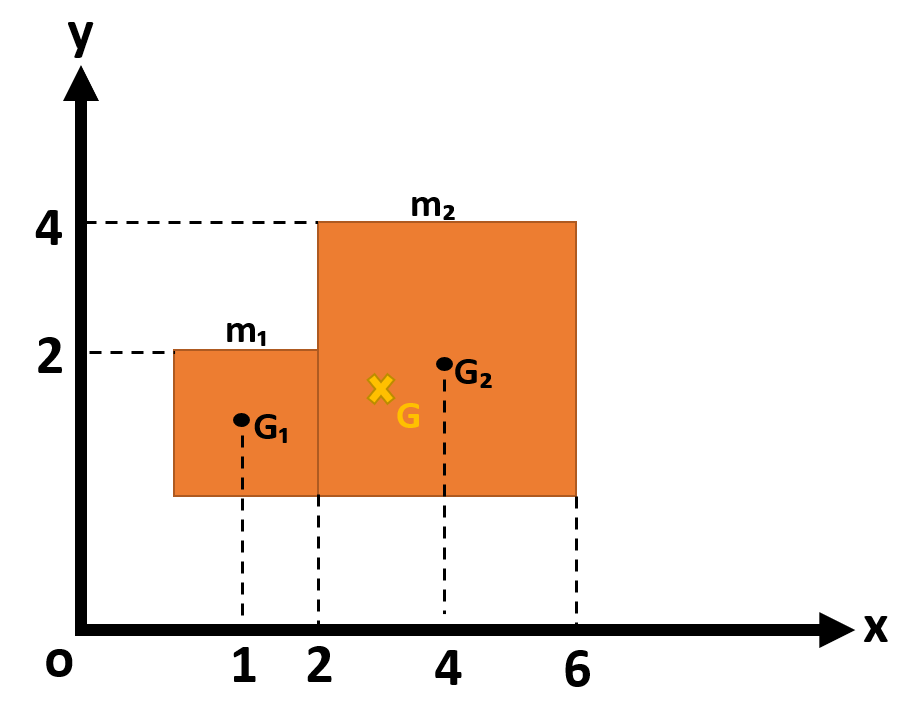
同じ材質でできた同じ厚さの正方形の板が2枚あります。
これらを図のようにx、y座標上に並べて置いた時、全体の重心の位置はどこになるか求めなさい。
なお、重心のx、y座標は分数で表してください。
【解答】
各板の質量は面積に比例します。
各板の重心は、それぞれの正方形の中心と考えて座標を決め、重心の座用を求める式を適用しましょう。
それぞれの正方形板の重心G₁、G₂の座標は、G₁(1,1)、G₂(4,2)です。
小さい正方形の質量をmとすれば、大きい正方形の質量は面積から考えて4mと分かります。
重心の座標(x,y)を求める式を適用すると、
x=(m×1+4m×4)/(m+4m)=17/5
y=(m×1+4m×2)/(m+4m)=9/5
解答:(17/5,9/5)
関連としては等分布荷重や等辺分布荷重などが、求める際には同じ考え方になります。
図心と重心の違い!重心の求め方も簡単にわかりやすく解説
重心と図心の違いは、重さを考慮しているかどうかということ!
同じ材質で作られた正方形や三角形などの物体は、【重心=図心】となる
材質が異なる物体、たとえば円の半分が鉄、半分が木でできていた場合、図心は円の中心ですが、重心は鉄(重い)のほうにズレる
以上です。
ありがとうございました。