射流とは？常流と射流の違いやフルード数との関係もわかりやすく簡単に！

今回のテーマは水理学で欠かせない【常流と射流の違い】

射流とは何？

常流と射流の違いや、射流とは？というこんな疑問に、フルード数との関係も絡めてわかりやすく簡単に解説していきます。

それではさっそく参りましょう、ラインナップは目次からどうぞ 🙂

射流とは？常流と射流の違いやフルード数との関係もわかりやすく簡単に！

まずはじめに、水路の流れのうち、水深が比較的浅く速度のはやい流れを射流、深い水深でゆっくりした流れを常流とよびます。

だけど速いとかゆっくりって…もっと具体的に教えてほしい

了解です☆流れの速度Vをもう少し厳密に区分してみましょう。

たとえば、流れている水路に小石を投げ入れて波を起こしたとします。

この場合、水面を伝わる波の速度Cは、

C＝√gh

で計算できます。

hは水深、gは重力加速度（9.8m/s²）です。

常流とは？

流れの速度が速いかゆっくりかは、投げ入れた小石で起きるこの波の速度Cを基準にします。

流れの速度Vが、波速Cよりも遅いとき、すなわち

V＜√gh

のときが常流です。

射流とは？

これに対して流れの速度Vが波速Cより速いとき、すなわち

V＞√gh

のときが射流です。

ちなみに常流と射流の境界である流れの速度Vと波速Cが等しくなるときを限界流と呼びます。

これらの関係性をまとめるとこんな感じ 🙂

一方で、常流、射流の話は土木でいうと水理学の内容になります。

水理学の公式などをまとめた記事もありますので、ぜひ併せてご確認ください。

常流と射流とフルード数とをわかりやすく簡単に解説

わたしと小鳥と鈴と…みたいなタイトルになっちゃいましたが…（笑）

気を取り直して、常流と射流とフルード数の関係を解説していきます。

常流、射流の区別を水路の流れの速さと波速の大小で表しましたが、フルード数とは、流れの速度Vと波速Cの比（無次元量）のことです。

F＝V/C＝V/√gh

つまり、フルード数Fが1より小さいときは常流、1より大きい場合が射流です。

常流や射流の違いによって、開水路の性質は大きく変わることになります。

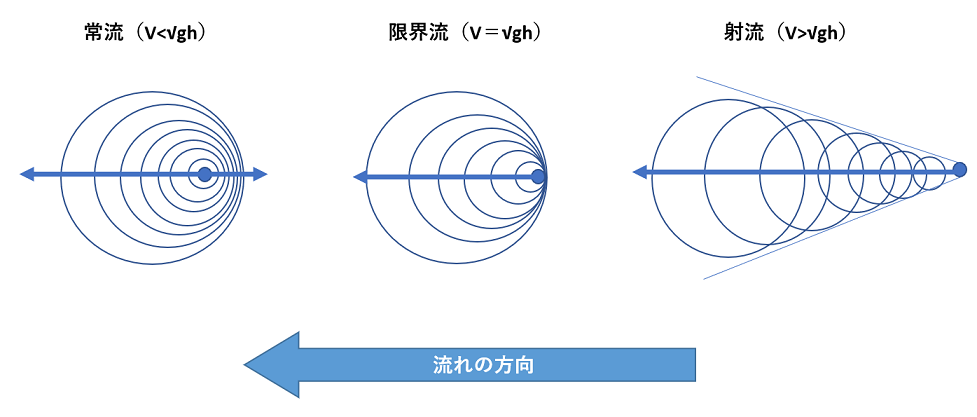
常流・射流・限界流の波の伝わり方

それぞれの流れについて、波の伝わり方の違いも見ていきましょう。

仮に流れのない水槽に石を投げいれると、波は同心円を描いて周囲に広がっていきます。

常流の場合は心が少しずつずれますが、上下流を含めて周囲に広がります。

これに対して射流の場合は、波は上流側に伝わらず、下流側のみに広がっていくのです。

このとき、波の円に接する線上に、衝撃波が発生しています。

射流とは？常流と射流の違いやフルード数との関係もわかりやすく簡単にまとめ

フルード数Fが1より小さいときは常流、1より大きい場合が射流

常流・射流・限界流 波の伝わり方

以上です。

興味のある方はぜひご覧ください。

ありがとうございました。

この記事を書いた人

名前：ちゃんさと