※この記事はプロモーションを含みます。
点高法とは測量や土木において、盛土または切土する敷地を長方形または三角形に分割し、計算によって必要な土量を求める計算方法です。
測量士補の試験にも出ますし、実務でも使われます。
土木学士である私がやり方やポイントをわかりやすく解説していきますので、試験勉強や実務の確認などにぜひご活用ください。
さらに読み方も要チェックです!
それではさっそく参りましょう、ラインナップは目次からどうぞ 🙂
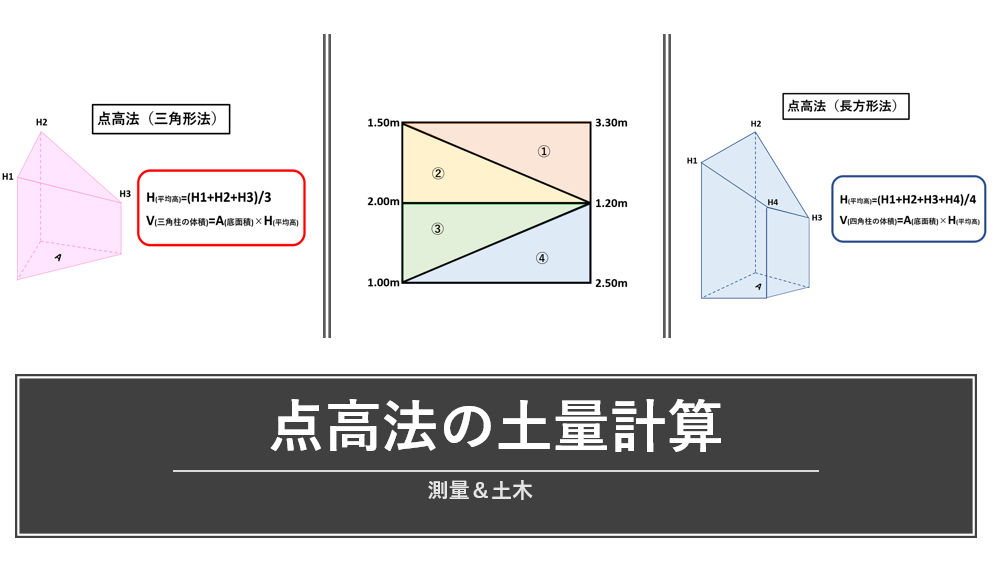
点高法のやり方や土量計算をわかりやすく解説!読み方も要チェック
まず、点高法の読み方は、「てんこうほう」です。
そして点高法による土量計算は、大きく分けて長方形法と三角形法の2つです。
点高法の種類
- 長方形法
- 三角形法
点高法のやり方➀長方形法
長方形法は、長方形や正方形に分割して行われます。
四角柱の体積は、【底面積×高さ】によって求めることができます。
しかし以下の図のように、四隅の高さがそれぞれ異なる場合は、平均高を求めてこれに底面積を掛け算することが必要です。
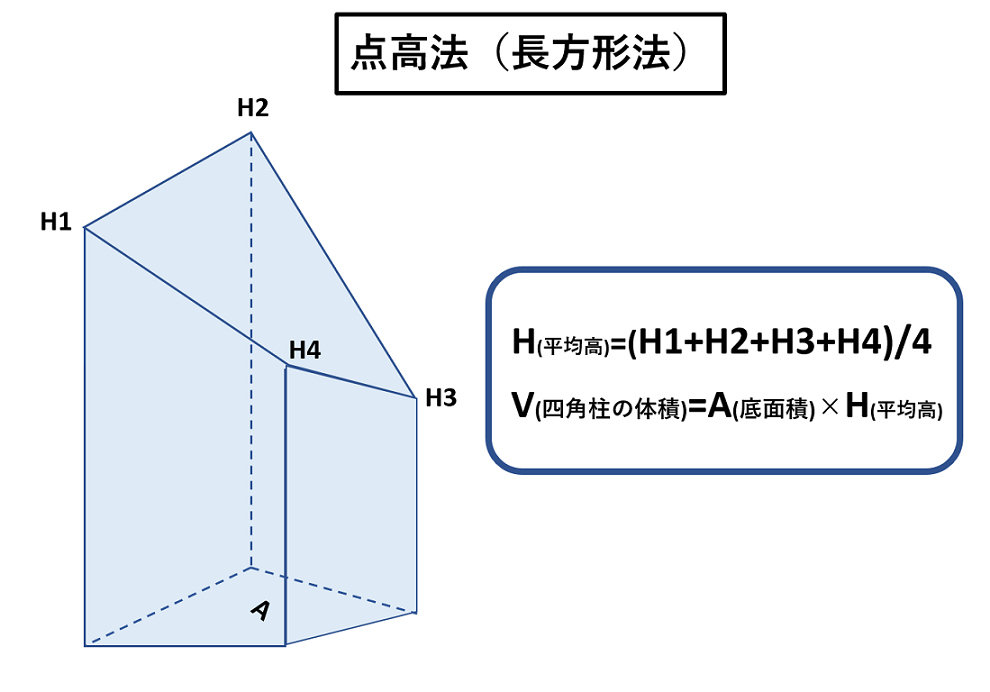
直方形法の計算公式
H(平均高)=(H1+H2+H3+H4)/4
V(四角柱の体積)=A(底面積)×H(平均高)
点高法のやり方②三角形法
三角形法も長方形法と考え方は同じ 😉
一般に三角柱の体積は【底面積×高さ】によって求めることができます。
しかし三隅の高さがそれぞれ異なる場合は、平均高さを求め、底面積を掛けましょう。
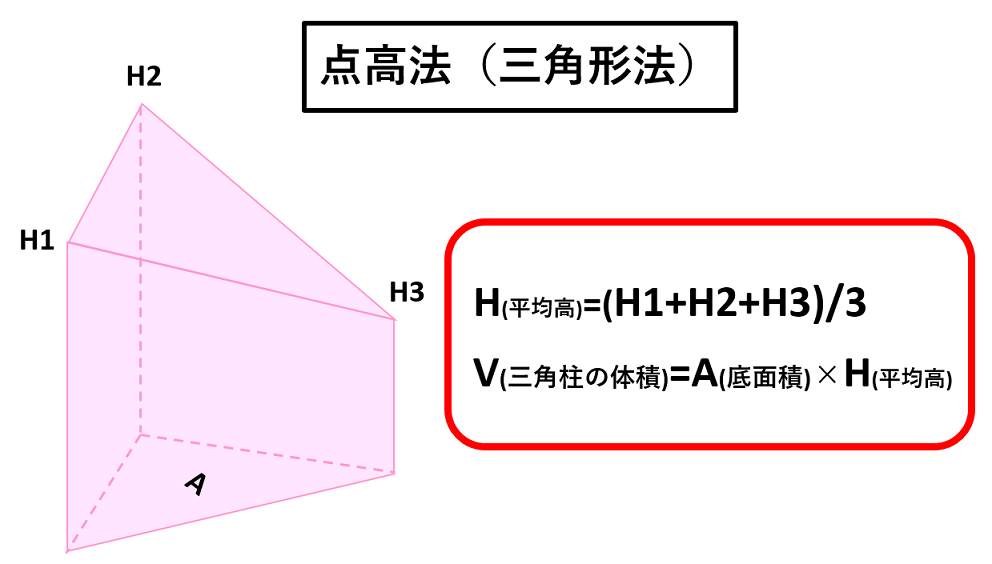
三角形法の計算公式
H(平均高)=(H1+H2+H3+H4)/3
V(三角柱の体積)=A(底面積)×H(平均高)
測量関連だとトラバース測量の計算方法も確認しておくと良いでしょう。
測量士補試験の例題!点高法による土量計算
ここでひとつ、例題を解いてみましょう。
測量士補の過去問題です。
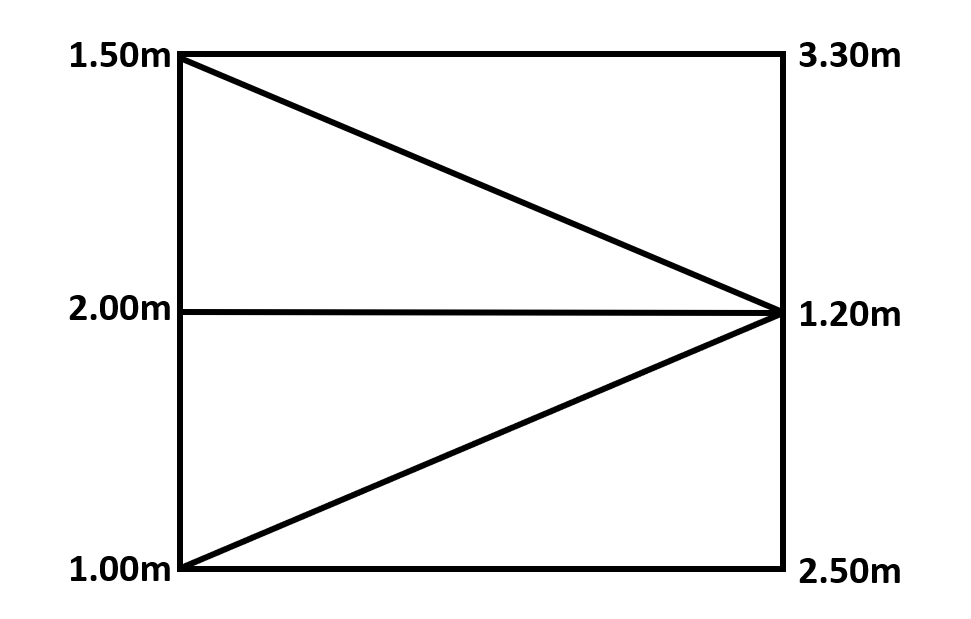
上記のような宅地造成予定地を、切土量と盛土量を等しくして平坦な土地に地ならしする場合、地ならし後における地盤高はいくつか。
最も近いものを次から選びなさい。
ただし上記の図のように、宅地造成予定地を面積の等しい4つの三角形に区分して点高法により求めるものとする。
また、図に示す数値は、各点の地盤高である。
- 1.63m
- 1.73m
- 1.84m
- 1.92m
- 2.03m
【解答】
問題文にあるように、それぞれ①~④の三角柱ととらえ、計算していきます。
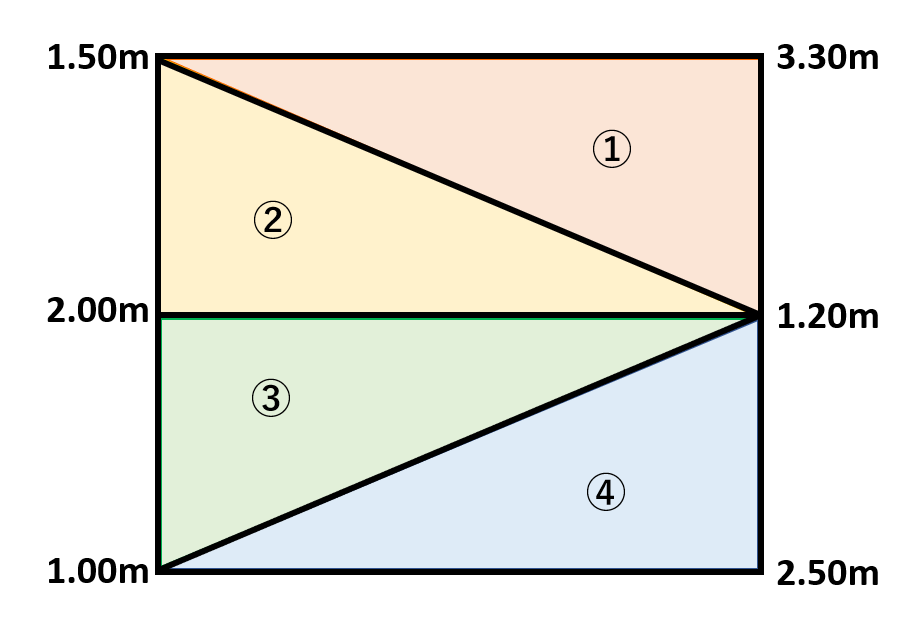
それぞれの平均地盤高は、
①三角形(オレンジ)の平均高さ
(1.50+3.30+1.20)/3=6/3=2.000
①⇒2.00m
②三角形(イエロー)の平均高さ
(1.50+2.00+1.20)/3=4.7/3=1.567
②⇒1.567m
③三角形(グリーン)の平均高さ
(2.00+1.20+1.00)/3=4.2/3=1.400
③⇒1.400m
④三角形(ブルー)の平均高さ
(2.00+1.20+2.50)/3=4.7/3=1.567
④⇒1.567m
①~④の平均高さは
(①2.00+②1.567+③1.400+④1.567)/4=6.534/4
=1.6335≒1.63m
よって答えは1
解答:1(1.63m)
併せて土量変化率計算についてもチェックしておきましょう。
また測量士補試験の受験を考えているのであれば、通信講座を比較した記事がおすすめです。
ぜひご確認ください。
点高法のやり方や土量計算をわかりやすく解説!読み方まとめ
点高法(てんこうほう)とは測量や土木において、盛土または切土する敷地を長方形または三角形に分割し、計算によって必要な土量を求める計算方法
点高法のやり方や計算式
| 点高法 | 平均地盤高 | 体積 |
|
直方形法
|
H(平均高)=(H1+H2+H3+H4)/4 | V(四角柱の体積)=A(底面積)×H(平均高) |
| 三角形法
|
H(平均高)=(H1+H2+H3+H4)/3 | V(三角柱の体積)=A(底面積)×H(平均高) |
以上です。
ありがとうございました。