※この記事はプロモーションを含みます。
座標法による面積計算は、計算表を作成し、それに数値を当てはめていくことで答えを導く方法です。
とくに測量士補の試験でもよく出題されますが、電卓の持ち込みは禁止されているので、計算ミスなどには注意してください。
また測量士補の試験を受けるのに、通信講座などをお考えでしたら、また別記事で比較していますのでご確認ください。
ちなみに1番のおすすめは、コスパ&合格率の高さからアガルートです。
ぜひ公式サイトをチェックしてみてくださいね 🙂
\アガルート公式サイト/
それでは話を元に戻して本題、本題っと。(笑)
例題を解きながら、座標法による面積計算をマスターしていきましょう 😉
ラインナップは目次からどうぞ!
座標法の面積計算や公式とは?測量士補試験にも出る面積計算&例題付き

座標法のほか平均断面法や点高法による土量計算などはまた別記事でご確認ください。
測量士補の例題①座標法による面積計算・XY座標の基礎

公式:Σ{(その点のX座標値)×(次の点のY座標値-1つ前の点のY座標値)}/2
ただちょっとわかりにくいので(笑)
ここでひとつ、例題をやってみましょう。
例題)境界点A、B、C、Dを結ぶ直線で囲まれた四角形の土地の測量を行い、表に示す平面直角座標系の座標値を得ました。この土地の面積を求めなさい。
| 境界点 | X座標(m) | Y座標(m) |
| A | -15.000 | -15.000 |
| B | +35.000 | +15.000 |
| C | +52.000 | +40.000 |
| D | -8.000 | +20.000 |
解答)
ふつうに座標点をとって面積を計算することもできますが、1箇所を0(原点)となるように考えるとより簡単に計算ができます。
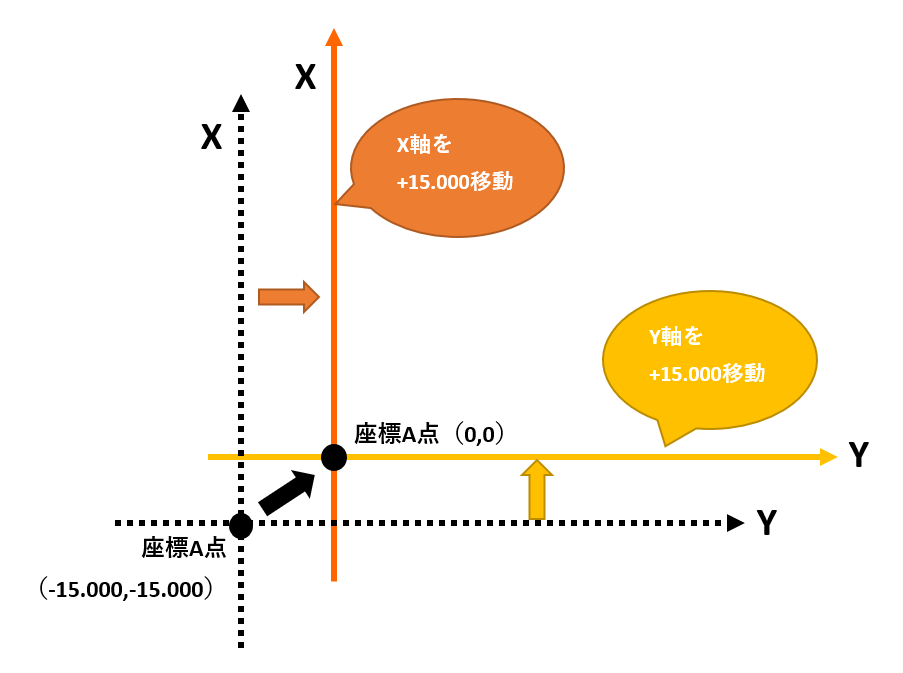
今回の場合は、X、Y座標値に+15.000をすると以下のようになり、Aの境界点を原点(0,0)として考えることができます。
| 境界点 | X座標(m) | Y座標(m) |
| A | -15.000+15.000=0.0 | -15.000+15.000=0.0 |
| B | +35.000+15.000=50.000 | +15.000+15.000=30.000 |
| C | +52.000+15.000=67.000 | +40.000+15.000=55.000 |
| D | -8.000+15.000=7.000 | +20.000+15.000=35.000 |
さらに計算表を作成し、座標法によって面積を求めましょう。
公式:Σ{(その点のX座標値)×(次の点のY座標値-1つ前の点のY座標値)}/2
| 境界点 | X座標(m) | Y座標(m) | (次の点のY座標値-1つ前の点のY座標値) | (その点のX座標値)×(次の点のY座標値-1つ前の点のY座標値) |
| A | 0.0 | 0.0 | 30(B)-35(D)=-5 | 0×(-5)=0 |
| B | 50.000 | 30.000 | 55(C)-0(A)=55 | 50×55=2,750 |
| C | 67.000 | 55.000 | 35(D)-30(B)=5 | 67×5=335 |
| D | 7.000 | 35.000 | 0-55=-55 | 7×(-55)=(-385) |
| 倍面積(合計) | 2,700 | |||
| 面積(倍面積÷2) | 1,350 | |||
よって点A、B、C、Dで囲まれた土地の面積は1,350㎡です。(解答)
解答:面積1,350㎡
測量士補の例題②座標法による面積計算・XY座標の応用
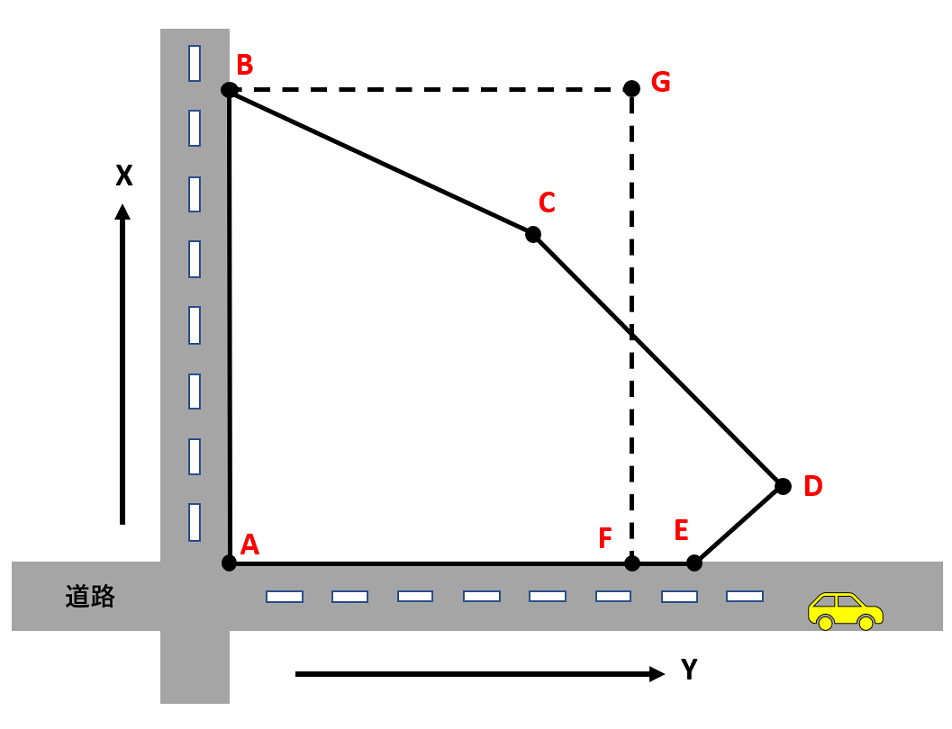
上記の図のように道路と隣接した土地に新たに境界線を引き、土地ABCDEを同じ面積の長方形ABGFに整正したい。
近傍の基準点に基づき、境界点A,B,C,D,Eを測定して平面直角座標系に基づく座標値を求めたところ、表に示す結果を得た。
| 点 | X座標 | Y座標 |
| A | -5.380 | -24.220 |
| B | +34.620 | -24.220 |
| C | +28.620 | +1.780 |
| D | +0.620 | +31.780 |
| E | -5.380 | +21.780 |
境界点GのY座標はいくらか。最も近いものを次の中からえらべ。
- +14.080m
- +14.920m
- +32.080m
- +38.300m
- +62.520m
【解答】
まずは座標原点を移動し、座標値を計算しやすい数値にすることがポイントです。
たとえばX座標に-0.620、Y座標に+0.220をすると、キレイな数字となり計算しやすくなります。
| 点 | X座標 | Y座標 |
| A | -5.380-0.620=-6.000 | -24.220+0.220=-24.000 |
| B | +34.620-0.620=34.000 | -24.220+0.220=-24.000 |
| C | +28.620-0.620=28.000 | +1.780+0.220=2.000 |
| D | +0.620-0.620=0.000 | +31.780+0.220=32.000 |
| E | -5.380-0.620=-6.000 | +21.780+0.220=22.000 |
つづいて以下のような計算表を作成し、数値を入れ、倍面積、面積を計算しましょう。
公式:Σ{(その点のX座標値)×(次の点のY座標値-1つ前の点のY座標値)}/2
| X | Y | (次の点のY座標値-1つ前の点のY座標値) | (その点のX座標値)×(次の点のY座標値-1つ前の点のY座標値) | |
| A | -6 | -24 | 24-22=-46 | -6×(-46)=276 |
| B | 34 | -24 | 2-(-24)=26 | 34×26=884 |
| C | 28 | 2 | 32-(-24)=56 | 28×56=1568 |
| D | 0 | 2 | 22-2=20 | 0×20=0 |
| E | -6 | 22 | -24-32=-56 | -6×(-56)=336 |
| 倍面積 | 3064 | |||
| 面積 | 1532 | |||

これらの結果より、A点とB点の距離はX軸に平行であるため、34.620-(-5.380)=40.000mとなります。
求めるべき土地A,B,G,Fは、問題文より長方形であるため、その面積は40m×αです。
土地の面積は変わらないため、先ほど求めた面積を用いて次の式を組み立てることができます。
1,532㎡=40.000m×α
したがってα=38.3m
境界点GのY座標は、点BのY座標値+38.3mとなるため、
点GのY座標=-24.220+38.300=14.080
よって点GのY座標は、+14.080mとなります。
最も近い選択肢は1です。
解答1(14.080m)
測量士補の例題③座標法による面積計算・方向角
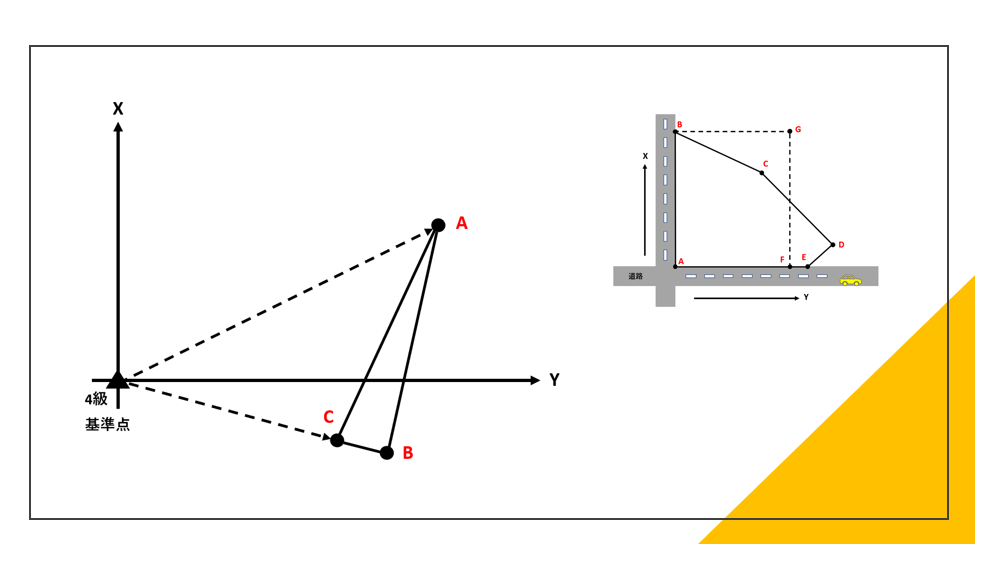
下に示す表は、公共測量により設置された4級基準点から図のように三角形の頂点に当たる地点A,B,Cをトータルステーションにより測量した結果を示しています。
| 地点 | 方向角 | 平面距離 |
| A | 75°00’00” | 48.000m |
| B | 105°00’00” | 32.000m |
| C | 105°00’00” | 23.000m |
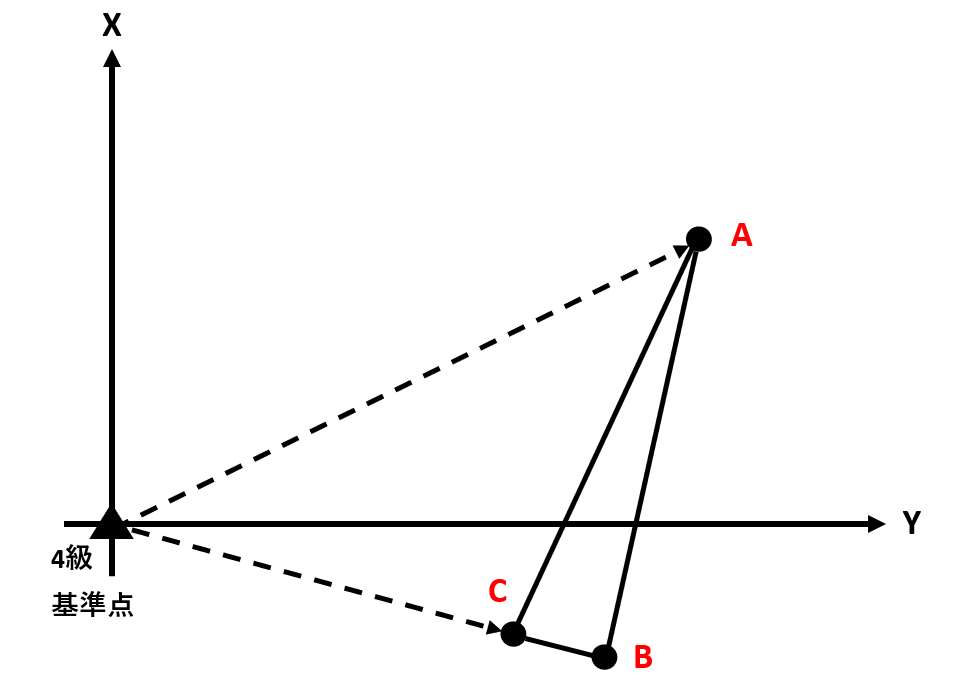
地点A,B,Cで囲まれた三角形の土地の面積はいくつか。最も近いものを次から選べ。
- 55.904㎡
- 108.000㎡
- 138.440㎡
- 187.061㎡
- 200.000㎡
【解答】
まずはsinθ、cosθを使って、地点A、B、Cの座標値を求めましょう。
| 地点 | X | Y | X=cosθ×キョリ | Y=sinθ×キョリ |
| A | 75°00’00” | 48.000m | 48×cos75°=12.423m | 48×sin75°=46.365m |
| B | 105°00’00” | 32.000m | 32×cos75°=8.282m | 32×sin75°=30.910m |
| C | 105°00’00” | 23.000m | 23×cos75°=5.953m | 23×sin75°=22.216m |
そして土地ABCの面積を求めるため、以下のような計算表を作成し、数値を記入して計算してください。
| X | Y | (次の点のY座標値-1つ前の点のY座標値) | (その点のX座標値)×(次の点のY座標値-1つ前の点のY座標値) | |
| A | 12.423 | 46.365 | 30.910-22.216=8.694 | 12.423×8.694=108.006 |
| B | -8.282 | 30.910 | 22.216-46.365=24.149 | -8.282×(-24.149)=200.002 |
| C | -5.953 | 22.216 | 46.365-30.910=15.455 | -5.953×15.455=-92.004 |
| 倍面積 | 216.004 | |||
| 面積 | 108.002 | |||
よって最も近いのは2となります。
解答2(108.000㎡)
座標法の面積計算や公式とは?測量士補試験にも出る面積計算まとめ
座標法の面積計算や公式についてのまとめです。
測量士補、測量士の試験にも出ますのでくりかえし問題を解いてみましょう。
ポイント
座標法による面積計算は、計算表を作成し、それに数値を当てはめていくことで答えを導く方法
公式:Σ{(その点のX座標値)×(次の点のY座標値-1つ前の点のY座標値)}/2
以上です。
ありがとうございました。