ネットワーク式工程表に関する問題を集めてみました。
解答・解説つきですので、ぜひチャレンジしてみてください。
一方で、ネットワーク工程表の解き方を勉強したい方は別記事でご確認ください。
ネットワーク式工程表の問題(例題)にチャレンジ!
問題は全部で6問あります。

ネットワーク式①工程の例題
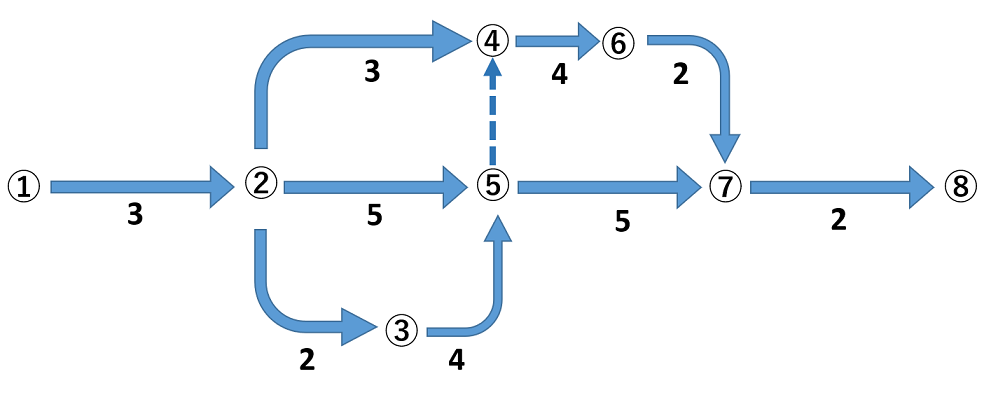
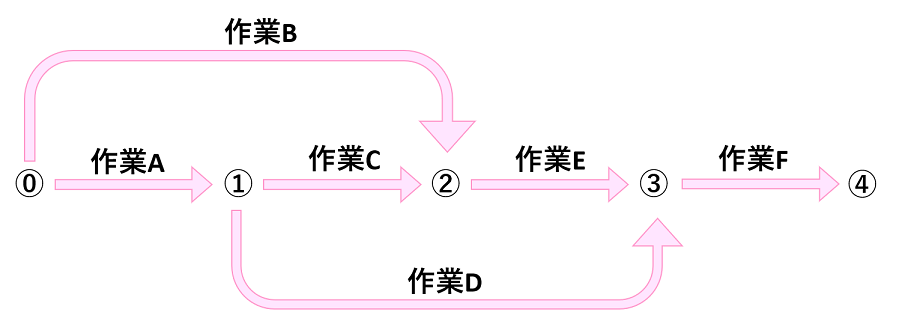
上記の図は、ある工事のネットワーク図です。
この工事の最短工期は何日か求めなさい。ただし、図の矢線上の数値はそこでの作業所要日数を、図の破線はダミーを示します。
ネットワーク式②工程の例題

上記のような工程からなる工事があります。
この工事に8人まで投入可能であるとしたとき、最小工期を求めなさい。ただし、図の矢線上の数値はそこでの作業所要日数を、図の破線はダミーを示します。
また、各工程は所要人数を確保しなければ施工できず、着工後はその工程を中断することはできないものとします。
ネットワーク式③工程の例題
| 作業 | 標準作業日数 | 標準作業から1日短縮するために必要な費用 |
| A | 5 | 3 |
| B | 8 | 4 |
| C | 4 | 5 |
| D | 7 | 2 |
| E | 5 | 6 |
| F | 3 | 7 |
上記の図は作業A~Fからなる工事のネットワーク図であり、表は作業A~Fの標準作業日数と標準作業日数から1日短縮するために必要な費用を示したものです。
このとき、この工事の工期を2日短縮するために必要な費用の最小値はいくらか、以下の選択肢から選びなさい。
ただし、各作業の作業日数は、標準作業日数から1日しか短縮できないものとします。
また作業A・Bは同時に開始でき、他の作業は先行する作業の終了と同時に開始できるものとします。
- 7万円
- 8万円
- 9万円
- 10万円
- 11万円
ネットワーク式④クリティカルパスの例題
| 工程 | 標準工程日数
【日】 |
各工程に要する1日当たりの費用 | |
| 標準工程
【万円/日】 |
標準工程から1日短縮した場合
【万円/日】 |
||
| A | 5 | 5 | 8 |
| B | 4 | 8 | 12 |
| C | 7 | 7 | 10 |
| D | 6 | 6 | 9 |
| E | 3 | 4 | 6 |
| F | 8 | 6 | 8 |
| G | 4 | 8 | 10 |
| H | 5 | 4 | 7 |
| I | 5 | 5 | 8 |
上記の図と表のようなネットワークがあります。
あるひとつの工程を標準工程と比較して1日短縮したところ、ネットワークの全体工期から1日短縮されました。
このとき、工程短縮による増加費用が最小であったとすると、どの工程を1日短縮したか答えなさい。
ネットワーク式工程表⑤正誤問題
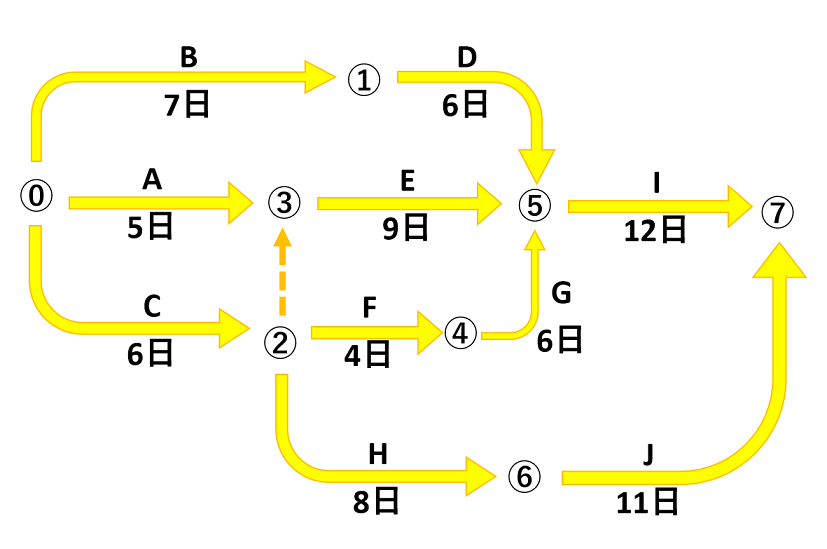
上記のネットワーク工程表で示される工事で、作業Eに3日間の遅れが生じた場合、次のうち適当なものはどれか選びなさい。
ただし、図中のイベント間のA~Jは作業内容、数字は当初の作業日数を表します。
- 当初の工期より1日遅れる
- 当初の工期より2日遅れる
- 当初の工期どおり完了する
- クリティカルパスの経路は当初と変わらない
ネットワーク式工程表⑥正誤問題
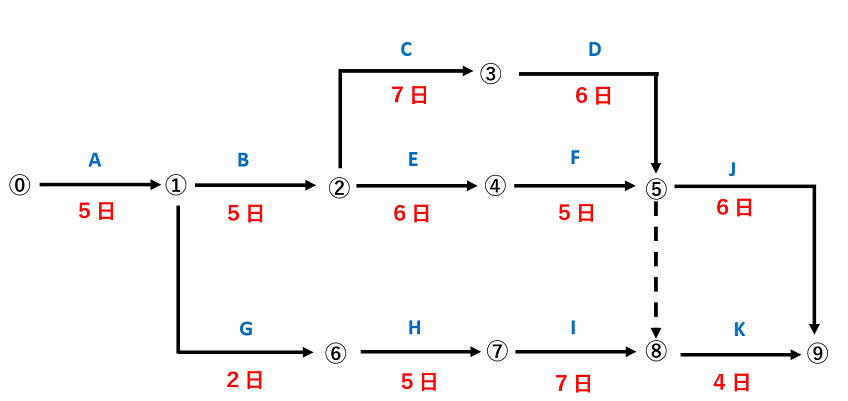
上記のネットワーク工程表に関する次の記述のうち、適当なものを1つ選びなさい。
- クリティカルパスは⓪→①→②→④→⑤→⑨である
- 作業Kの最早開始日は、工事開始後19日である
- ①→⑥→⑦→⑧の作業余裕日数は4日である
- 工事開始から工事完了までの必要日数(工期)は27日である
ネットワーク式工程表!問題(例題)の解答・解説

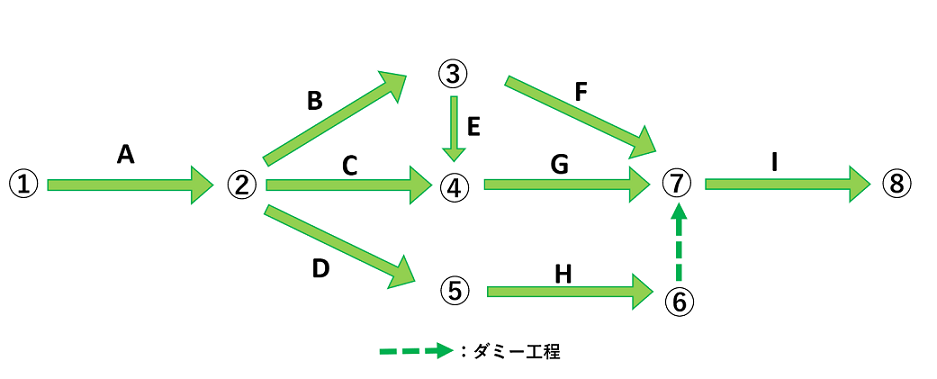
ネットワーク式①工程の例題

破線→のダミー作業は実体のない作業です。
それゆえ所要日数は0ですが、作業④-⑥は、作業②-④、作業②-⑤ならびに③-⑤が終了しないと開始することができません。
一方で、
①-②-④の日数は3+3=6日
①-②-⑤の日数は3+5=8日
①-②-③-⑤の日数は3+2+4=9日
であるため、作業④-⑥は9日後にしか開始できません。
したがって所要日数は、
9+4(④-⑥)+2(⑥-⑦)+2(⑦-⑧)=17日
となります。
ネットワーク式②工程の例題

与えられた工事の所要日数を計算すれば、
⓪→②→③が15日+7日=22日
⓪→①→②→③が7日+7日+7日=21日
⓪→①→③が7日+13日=20日
工事には8人までしか投入できないため、工事⓪→①→③の①→③は、工事⓪→①→②→③の①→②(所要日数7日)を終了してからでないと開始できません。
したがって、この工事の最小工期は20+7日となります。
ネットワーク式③工程の例題
| 作業 | 標準作業日数 | 標準作業から1日短縮するために必要な費用 |
| A | 5 | 3 |
| B | 8 | 4 |
| C | 4 | 5 |
| D | 7 | 2 |
| E | 5 | 6 |
| F | 3 | 7 |
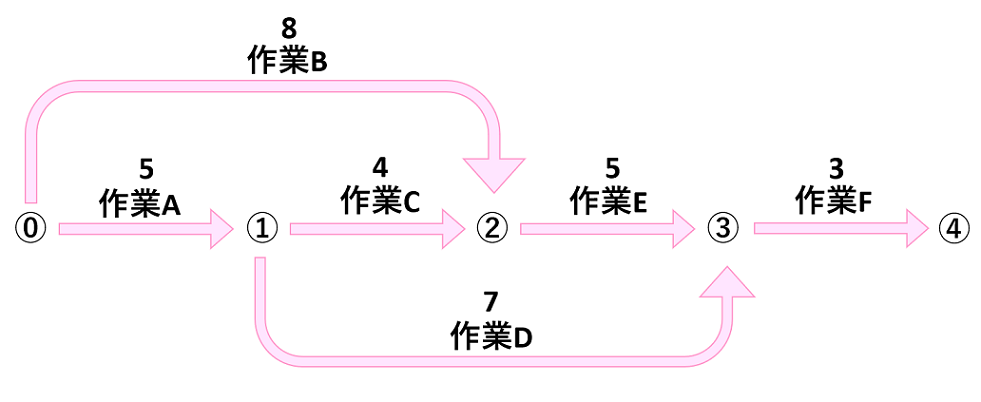
作業日数を入れ込んだ上記の図から、
作業Aと作業Cで、必要費用の安い作業Aを1日短縮すれば3万円増加
作業Eと作業Fで、必要費用の安い作業Eを1日短縮すれば6万円増加
すなわち、この工事の工期を2日短縮するために必要な費用の最小値は9万円であることが分かります。
ネットワーク式④クリティカルパスの例題

| 工程 | 標準工程日数
【日】 |
各工程に要する1日当たりの費用 | |
| 標準工程
【万円/日】 |
標準工程から1日短縮した場合
【万円/日】 |
||
| A | 5 | 5 | 8 |
| B | 4 | 8 | 12 |
| C | 7 | 7 | 10 |
| D | 6 | 6 | 9 |
| E | 3 | 4 | 6 |
| F | 8 | 6 | 8 |
| G | 4 | 8 | 10 |
| H | 5 | 4 | 7 |
| I | 5 | 5 | 8 |
まずはそれぞれのルートについて、標準工程日数の合計を計算すれば、クリティカルパスは
①→②→③→⑦→⑧であることが分かります。
そこで、工程A、B、F、Iについて、工程短縮による増加費用を求めると、
工程A=8×(5-1)-5×5=7万円
工程B=12×(4-1)-4×8=4万円
工程F=8×(8-1)-8×6=8万円
工程I=8×(5-1)-5×5=7万円
したがって、増加費用が最小となる工程はBであることが分かります。
ネットワーク式工程表⑤正誤問題

- 当初の工期より1日遅れる:×→遅れは2日なので適当ではない
- 当初の工期より2日遅れる:○
- 当初の工期どおり完了する:×→遅れが2日出るので適当でない
- クリティカルパスの経路は当初と変わらない:×→クリティカルパスは⓪→②→④→⑤→⑦から、⓪→②→③→⑤→⑦に変化するので適当ではない
よって解答は2が正解です。
ネットワーク式工程表⑥正誤問題

- クリティカルパスは⓪→①→②→④→⑤→⑨である:×クリティカルパスは最長の所要日数であるため、⓪→①→②→③→⑤→⑨である
- 作業Kの最早開始日は、工事開始後19日である:×→最早開始日は、工程が複数ある場合は最長の所要日数であるため、⓪→①→②→③→⑤→⑧の23日である
- ①→⑥→⑦→⑧の作業余裕日数は4日である:○→所要日数①→⑥→⑦→⑧の所要日数は19日で⑧の作業余裕日数は23日なので、23日-19日=4日
- 工事開始から工事完了までの必要日数(工期)は27日である:×→工事完了までの必要日数(工期)は、クリティカルパス上の所要日数となるため、⓪→①→②→③→⑤→⑨=29日となる
以上です。
ありがとうございました。