図心とは、図形の面積が平均的に集まっている位置、いわば「形の中心」を示す点です。
構造計算や断面計算では、モーメントや応力度を求める基準となる重要なポイントになります。
基本図形なら公式で求められ、複雑な形でも分割やくり抜きの考え方を使えば計算できます。
この記事では、図心の意味から求め方までを図解つきでわかりやすく解説します。
図心とは?
図心とは、図形の「重さの中心」にあたる点のことです。
紙で作った図形を指先で支えたとき、ちょうどバランスが取れて倒れない場所を想像するとわかりやすいでしょう。
見た目の真ん中にあるように思えるかもしれませんが、図形の形によって図心の位置は変わります。
たとえば、長方形の図心は縦と横のちょうど真ん中にあります。
一方、三角形の場合は、3つの頂点から引いた「中線」が交わる点が図心となり、見た目の中心よりやや下に位置します。
さらに、複雑な形の図形では、図心が直感とは違う場所に来ることもあります。
また図心のほか、「重心」という言葉もありますが、この違いは重さを考えるかどうかです。
密度が同じであれば、図心=重心となりますが、例えば、図形の一部の材質(密度)が異なる場合などは、図心≠重心となりますのでご注意下さい。
図心と重心の違いについては以下の記事をご覧ください。
基本図形の図心位置
基本図形については公式で図心位置が決まっています。
長方形
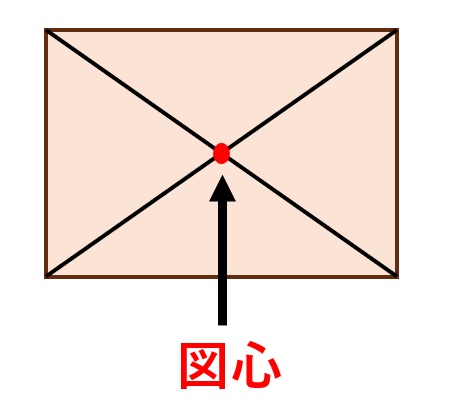
長方形は、たて・よこの真ん中が図心になります。
三角形
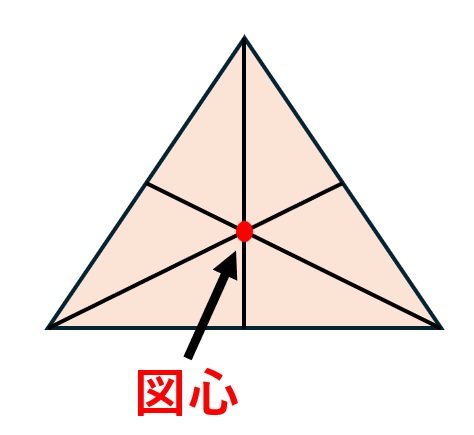
三角形の図心は3つの頂点から引いた「中線」が交わる点になります。
底辺から高さ1/3のところです。
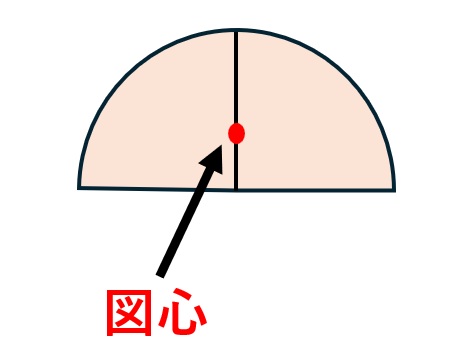
円形・半円
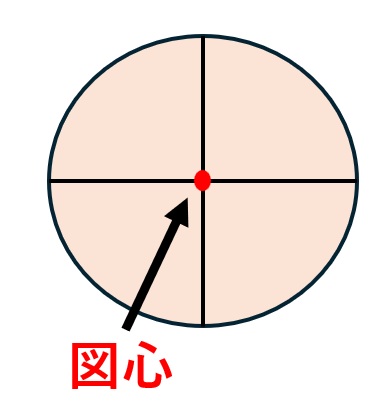
円の図心は中心です。
そして半円だと底辺から4r/3πのところが図心となります。
図心の求め方|計算問題を例題でチェック
様々な図形で図心を求めていきましょう。
段付き断面の図心の求め方
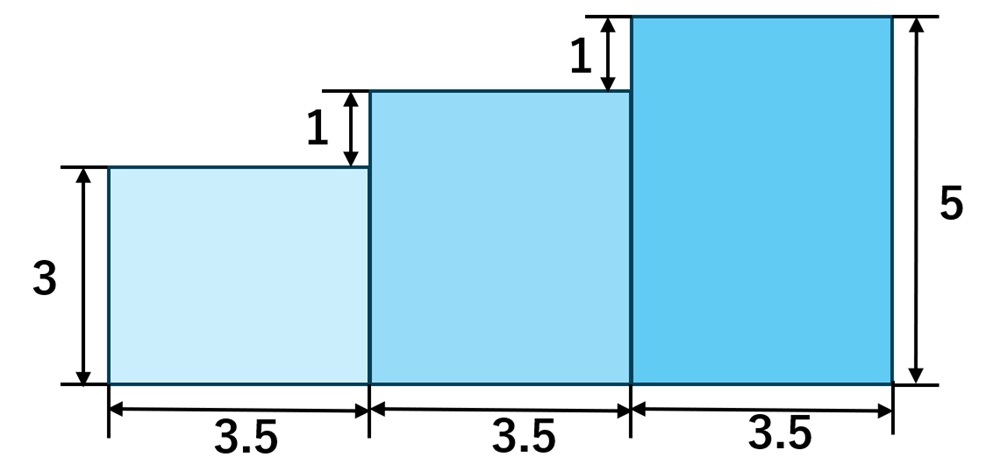
この段付き図形は、横に並んだ長方形3つの合成断面として求めます。
左下を原点 (0,0)、下端を y=0 として計算していきましょう。
分割(3つの長方形)
幅はすべて 3.5。高さは段ごとに 3 → 4 → 5。
| 部分 | 幅 | 高さ | 面積A |
|---|---|---|---|
| ① 左 | 3.5 | 3 | 10.5 |
| ② 中 | 3.5 | 4 | 14 |
| ③ 右 | 3.5 | 5 | 17.5 |
合計面積
A=42
各部分の図心座標
x座標(左端から)各長方形の中心は以下のとおり。
- x₁ = 1.75
- x₂ = 3.5 + 1.75 = 5.25
- x₃ = 7.0 + 1.75 = 8.75
y座標(下端から)は以下のとおりです。
- y₁ = 3/2 = 1.5
- y₂ = 4/2 = 2.0
- y₃ = 5/2 = 2.5
そして図心の公式と計算方法はこちらです。

よって解答は図心座標(x,y)=(5.83, 2.08)となります。
T型の図心の求め方
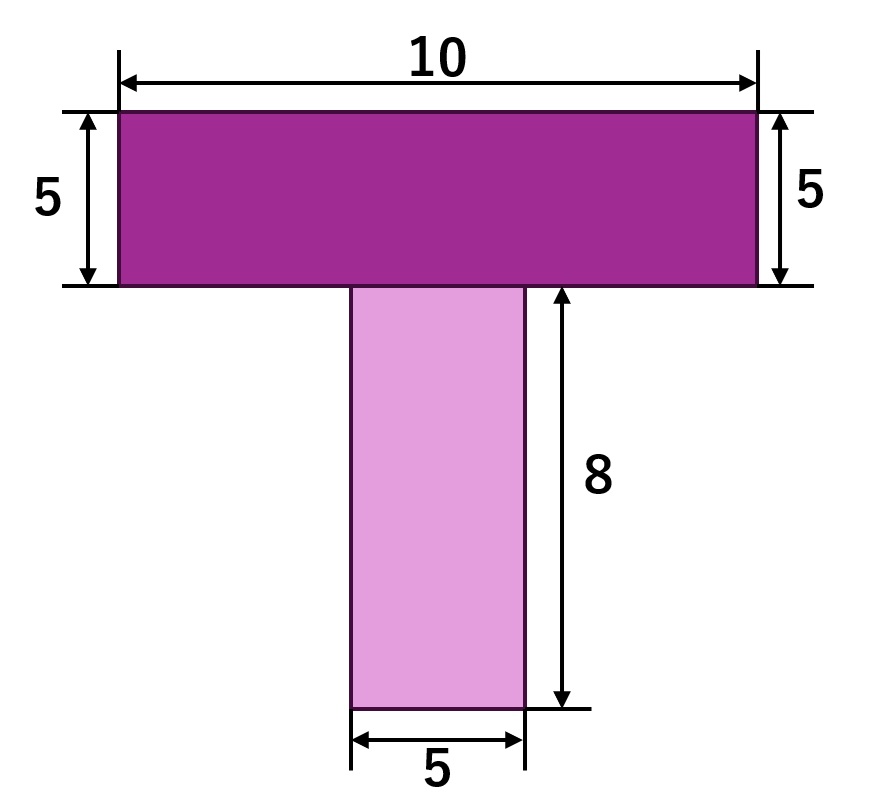
T形断面の図心は、フランジとウェブに分割し、面積×距離の合計(断面一次モーメント)を全面積で割ることで求めることができ、左右対称の場合、横座標は中央線上になります。
このT形断面は 長方形2つに分けて断面一次モーメントで計算します。
左右対称なので、図心の x 座標は中央線上です。(横方向は自動的に中央(幅10の中心)になります。)
ここでは いちばん下を基準(y=0) として縦座標を求めます。
【図形の分割】
① 上のフランジ(横長)
- 幅10 × 高さ5
- 面積 A₁ = 50
② 下のウェブ(縦)
- 幅5 × 高さ8
- 面積 A₂ = 40
各部分の図心の位置(下端からの距離)
■ ウェブ
高さ8 → 中心は
y₂ = 8/2 = 4
■ フランジ
ウェブの上に載っているので
下端から 8 上にある
高さ5 の中心 → 2.5 上
y₁ = 8 + 2.5 = 10.5
断面一次モーメントで計算
.jpg)
よって図心の位置は、下端からy=7.61となります。
全高は 13(=5+8)なので上端からは13 − 7.61 =約 5.39の位置です。
L型の図心の求め方
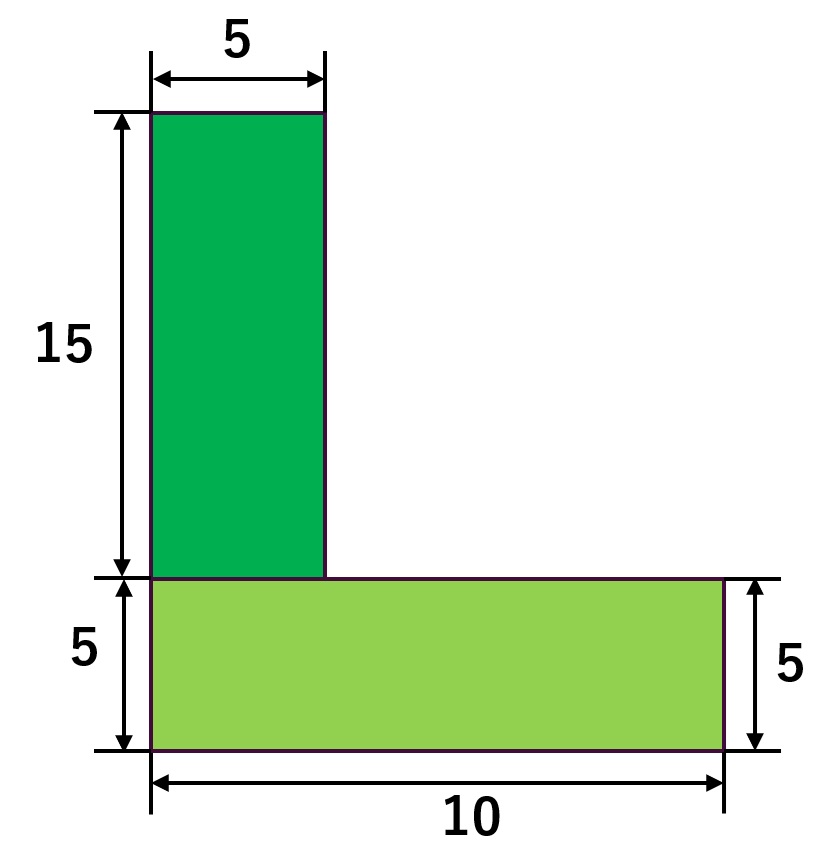
L形断面なので、長方形2つに分けて図心(=面積の加重平均)で計算します。
ここでは左下の外角を原点 (0,0) として座標で出します。
【図形を分割】
① 下の横長長方形
- 幅 10 × 高さ 5
- 面積 A₁ = 50
② 左の縦長長方形
- 幅 5 × 高さ 15(下の長方形の上に乗っている)
- 面積 A₂ = 75
合計面積
A = 125
各部分の図心座標
■① 下の長方形
中心:
x₁ = 10/2 = 5
y₁ = 5/2 = 2.5
■② 左の縦長長方形
下端は y = 5 の位置から始まる
高さ15の中心 → 7.5 上
x₂ = 5/2 = 2.5
y₂ = 5 + 7.5 = 12.5
.jpg)
よって解答は図心座標(x,y)=(3.5, 8.5)となります。
コ型(U型)の図心の求め方
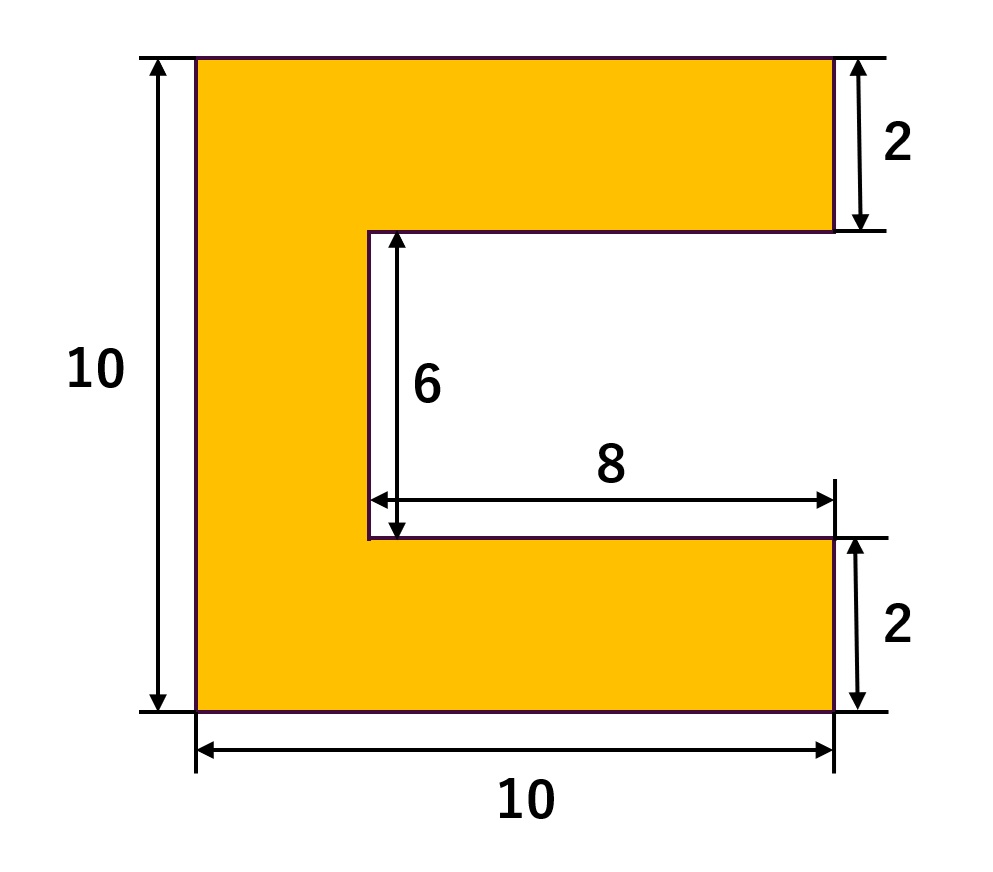
この図形は **マイナス方式(外側 − 内側の長方形)**で求めるのが最短です。
左下の外角を原点 (0,0) として計算します。
✅ 手順:外形 − くり抜き
■ 外側の長方形
- 幅 10 × 高さ 10
- 面積 A₁ = 100
- 図心:(5 , 5)
■ 内側のくり抜き長方形
図から:
- 幅 = 8
- 高さ = 6
- 左からの位置 = 2(=10−8)
- 下からの位置 = 2(=上下の厚み2ずつ)
- 面積 A₂ = 48
- 図心:
- x₂ = 2 + 8/2 = 6
- y₂ = 2 + 6/2 = 5
※くり抜きなので マイナス面積
合計面積はA = 100 - 48 = 52となります。
.jpg)
よって解答は図心座標(x,y)=(4.08, 5.00)となります。
