
こんなお悩みに 🙂
品質管理などでよく使う管理図について、種類や覚え方、見方をまとめましたので参考にしてください。
また例題もありますので、ぜひやってみてくださいね。係数表の使い方も要チェックです。
それではさっそく参りましょう、ラインナップはこちらです。
管理図の種類の覚え方&見方!例題で係数表の使い方ていねい解説
管理図の種類はこんな感じ 🙂
計数値と計量値の2種類に分類できます。
| 計数値の管理図(離散的な値) | 概要 |
| P管理図 | 不良率の管理図
不適合率を用いて工程を評価する |
| nP管理図 | 不良個数の管理図
不適合数を用いて工程を評価する |
| c管理図 | 欠点数の管理図
サンプルの不適合数を用いて工程を評価する |
| u管理図 | 単位当たり欠点数の管理図
サンプルの単位当たりの不適合数を用いて工程を評価する |
| 計量値の管理図(連続的な値) | 概要 |
| 個々の測定値を用いて工程を管理する
一点管理図ともいう |
|
| 平均値と範囲の管理図
群の平均値と範囲を用いて、工程の分散を評価する |
|
| 個々の測定値と範囲、試験誤差を用いて工程を評価する | |
| メディアンと範囲の管理図
メディアンを用いて群間のちがいを評価する |
これらの管理図はJISに規定されています。
ちなみに土木(建設業)では、![]() と
と![]() が比較的多く使われますよ 🙂
が比較的多く使われますよ 🙂
そしてここで、管理図のなかでもよく使う、シューハート管理図の覚え方と求め方についてみていきます。
| 管理図の種類 | 管理図計算式 | ||
| 中心線(CL) | 上方管理限界線(UCL) | 下方管理限界線(LCL) | |
| X管理図 | 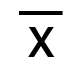 |
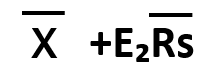 |
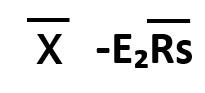 |
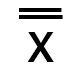 |
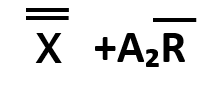 |
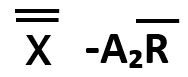 |
|
| R管理図 |  |
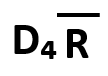 |
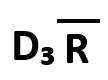 |
| Rs管理図 | 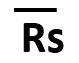 |
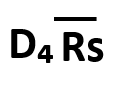 |
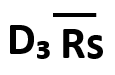
=考えない |
| Rm管理図 | 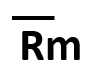 |
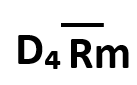 |
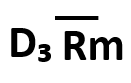 =考えない =考えない |
それぞれの管理図における
- 中心線(CL)
- 上方管理限界線(UCL)
- 下方管理限界線(LCL)
の式は上記のとおりです。
この式はこういうもんだと思って表をまるごと暗記しちゃったほうが早いかもしれません。(笑)
じっさい、R、Rs、Rmの式はほぼ同じなのでひとつ覚えればOKです。
X管理図と![]() 管理図のE₂とA₂をまちがえないようにすれば、なんとかなります 🙄
管理図のE₂とA₂をまちがえないようにすれば、なんとかなります 🙄
またA₂、D₄、D₃、E₂は、品質管理係数です。
表があるはずなので、数字はおぼえなくてOK!
係数表を確認してください。
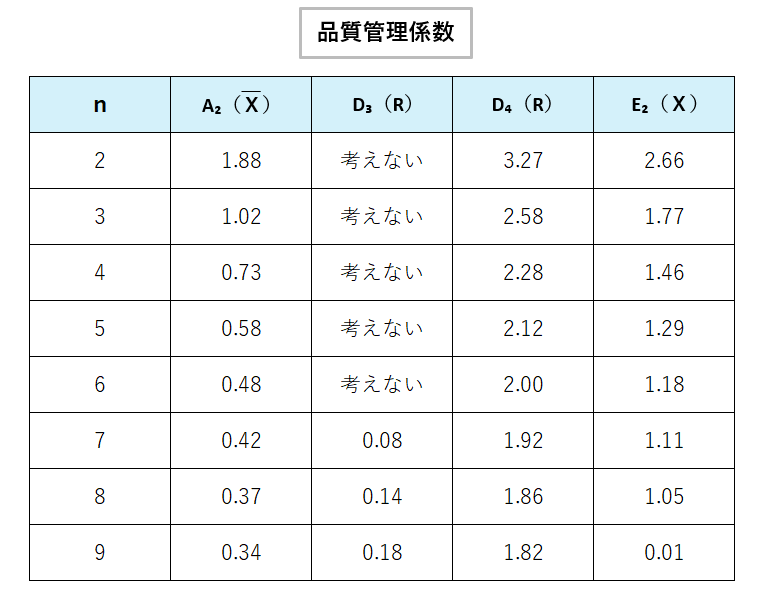
また、各記号の意味(式)はこんな感じです。
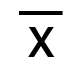 |
各試験データの平均 |
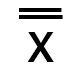 |
|
 |
各組R(範囲:最大値と最小値の差)の平均 |
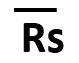 |
データの移動誤差(相となり合ったデータ差の絶対値) |
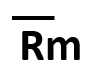 |
各組Rm(各組のデータの最大値と最小値の差=範囲) |


Ⅹ管理図の例題
| 中心線(CL) | 上方管理限界線(UCL) | 下方管理限界線(LCL) |
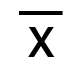 |
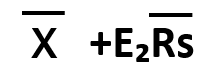 |
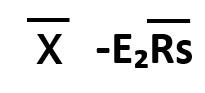 |
X管理図は、試料数が少ない場合に使われます。
たとえばコンクリートの強度試験で、3個のテストピースの平均値を1個のデータとするケースを想定してみます。
| ①テストピース | ②テストピース | ③テストピース | 平均 | |
| No.1 | 56 | 54 | 55 | 55 |
| No.2 | 59 | 54 | 58 | 57 |
| No.3 | 55 | 57 | 53 | 55 |
| No.4 | 53 | 53 | 54 | 53 |
| No.5 | 54 | 52 | 59 | 55 |
1)![]() (エックスバー)を求める
(エックスバー)を求める
No.1~No.5までの各試験のデータを平均する
![]() =(55+57+55+53+55)/5=55
=(55+57+55+53+55)/5=55
2)![]() を求める
を求める
![]() はデータの移動誤差(相となり合ったデータの差の絶対値)です。
はデータの移動誤差(相となり合ったデータの差の絶対値)です。
よって、|となり合った平均値の差|を計算すると
|55-57|=2
|57-55|=2
|55-53|=2
|53-55|=2
![]() =(2+2+2+2)/4=2
=(2+2+2+2)/4=2
3)E₂を求める
1回の試験で前データは3つとりますが、真のデータは1個であるのでn=1です。
ただし、管理係数表にn=1はないので、最小n=2を採用してE₂=2.66となります。

これらの求めたデータをX管理図の中心線(CL)、上方管理限界線(UCL)、下方管理限界線(LCL)にあてはめます。
CL=![]() =55
=55
UCL=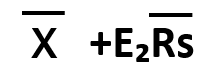 =55+2.66×2=60.32
=55+2.66×2=60.32
LCL=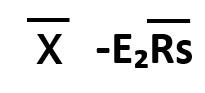 =55-2.66×2=49.68
=55-2.66×2=49.68
となります。
Xバー管理図の例題
| 中心線(CL) | 上方管理限界線(UCL) | 下方管理限界線(LCL) |
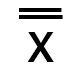 |
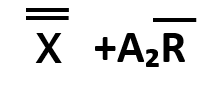 |
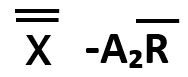 |
サンプルデータは以下のとおりとします。(データn=3)
| 試験回数 | 試料① | 試料② | 試料③ |
| 1 | 56 | 54 | 55 |
| 2 | 59 | 54 | 58 |
| 3 | 55 | 57 | 53 |
| 4 | 52 | 53 | 54 |
| 5 | 54 | 52 | 59 |
1)総平均![]() (エックストゥーバー)を求める
(エックストゥーバー)を求める
![]() を求めるために、各組の
を求めるために、各組の![]() を計算する(
を計算する(![]() は
は![]() をさらに平均した値)
をさらに平均した値)
1回目![]() =(56+54+55)/3=55
=(56+54+55)/3=55
2回目![]() =(59+54+58)/3=57
=(59+54+58)/3=57
3回目![]() =(55+57+53)/3=55
=(55+57+53)/3=55
4回目![]() =(52+53+54)/3=53
=(52+53+54)/3=53
5回目![]() =(54+52+59)/3=55
=(54+52+59)/3=55
よって、
![]() =(55+57+55+53+55)/5=55
=(55+57+55+53+55)/5=55
2)範囲の平均![]() を求める
を求める
![]() は各組のR(範囲)を平均することにより求められます。
は各組のR(範囲)を平均することにより求められます。
1回目 R=56-54=2
2回目 R=59-54=5
3回目 R=57-53=4
4回目 R=54-52=2
5回目 R=59-52=7
よって、
![]() =(2+5+4+2+7)/5=4
=(2+5+4+2+7)/5=4
3)管理限界係数A₂を求める
データn=3なので、品質管理係数表より、A₂=1.02となります。

これらの求めたデータをX管理図の中心線(CL)、上方管理限界線(UCL)、下方管理限界線(LCL)にあてはめます。
CL=![]() =55
=55
UCL=![]() =55+1.02×4=59.08
=55+1.02×4=59.08
LCL=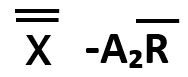 =55-1.02×4=50.92
=55-1.02×4=50.92
となります。
R管理図の例題
| 中心線(CL) | 上方管理限界線(UCL) | 下方管理限界線(LCL) |
 |
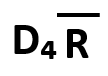 |
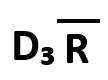 |
サンプルデータは以下のとおりとします。(データn=3)
| 試験回数 | 試料① | 試料② | 試料③ |
| 1 | 56 | 54 | 55 |
| 2 | 59 | 54 | 58 |
| 3 | 55 | 57 | 53 |
| 4 | 52 | 53 | 54 |
| 5 | 54 | 52 | 59 |
1)![]() を求める
を求める
![]() は各組のR(最大値と最小値の差)を平均して求めます。
は各組のR(最大値と最小値の差)を平均して求めます。
1回目 R=56-54=2
2回目 R=59-54=5
3回目 R=57-53=4
4回目 R=54-52=2
5回目 R=59-52=7
よって、
![]() =(2+5+4+2+7)=4
=(2+5+4+2+7)=4
2)係数D₄を求める
試料データn=3であるので、係数表よりD₄=2.58となります。
ただし、D₃はn≦6では負となるため、下方管理限界線は考えません。

これらの求めたデータをX管理図の中心線(CL)、上方管理限界線(UCL)、下方管理限界線(LCL)にあてはめます。
CL=![]() =4
=4
UCL=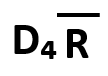 =2.58×4=10.32
=2.58×4=10.32
LCL=なし(考えない)
となります。
Rs管理図の例題
Rs管理図は1回の試験でデータをひとつしかとらない場合に、1個1個のデータの差(移動誤差=Rs)の動きをみて、工程の安定を確かめるために利用されます。
| 中心線(CL) | 上方管理限界線(UCL) | 下方管理限界線(LCL) |
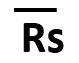 |
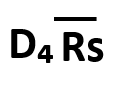 |
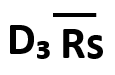
=考えない |
1)![]() を求める(Rsはとなり合った2個のデータ差=移動誤差)
を求める(Rsはとなり合った2個のデータ差=移動誤差)
| 55 | 58 | 59 | 54 | 57 |
| 3 | 1 | 5 | 3 |
![]() =(3+1+5+3)/4=3
=(3+1+5+3)/4=3
2)係数D₄を求める
R₂はとなり合った2個のデータ差(絶対値)であるので、Rsが計算されたベースとなるデータ数nは2となります。(n=2)
よって係数表によりn=2のD₄=3.27を採用します。

これらの求めたデータをX管理図の中心線(CL)、上方管理限界線(UCL)、下方管理限界線(LCL)にあてはめます。
CL=![]() =3
=3
UCL=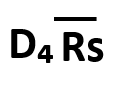 =3.27×3=9.81
=3.27×3=9.81
LCL=なし(考えない)
となります。
Rm管理図の例題
Rm管理図は、データ数が3以下の場合に使われます。
たとえば、コンクリート強度試験のように、1回の試験で3個のデータを採る場合のときなどです。
基本的にはR管理図とおなじで、各組データの最大値と最小値を用います。
| 中心線(CL) | 上方管理限界線(UCL) | 下方管理限界線(LCL) |
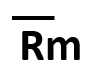 |
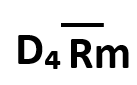 |
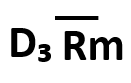 =考えない =考えない |
データ例)
| データ | a | b | c |
| No.1 | 180 | 185 | 187 |
| No.2 | 182 | 184 | 180 |
| No.3 | 185 | 189 | 181 |
1)![]() を求める
を求める
まずRm(各組の最大と最小の差)を計算し、その結果を平均します。
No.1Rm=187-180=7
No.2Rm=184-180=4
No.3Rm=189-181=8
![]() =(7+4+8)/3≒6.3
=(7+4+8)/3≒6.3
2)係数D₄を求める
n=3なので、係数表よりD₄=2.58を採用します。

これらの求めたデータをX管理図の中心線(CL)、上方管理限界線(UCL)、下方管理限界線(LCL)にあてはめます。
よって、
CL=![]() =6.3
=6.3
CL=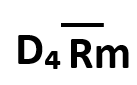 =2.58×6.3≒16.2
=2.58×6.3≒16.2
LCL=なし(考えない)
となります。
管理図の見方のコツ
管理図には管理限界線があります。
管理限界線は、品質のバラツキが通常起こるものなのか(偶然原因)、あるいは見逃せないバラツキであるか(異常原因)を判断する基準となるものです。
| 管理限界線 | |
| UCL | 上方管理限界線 |
| CL | 中心線(規格値平均) |
| LCL | 下方管理限界線 |
また、工程が安定していると判断できる基本条件はこちら
工程安定の基本条件
- 打点がすべて管理限界線のなかに入っている
- 点の並び方にクセがない
さらに以下の場合は、工程に異常がなく安定していると判断でき、管理線を延長して管理用に使うことができます。
- 点が連続25点以上管理限界内にある
- 連続35点中、限界外に出たものが1点以内
- 連続100点中、限界外に出たものが2点以内
いっぽう次の場合は、工程が不安定であると判断すべき状態を表しています。
| 工程が不安定と判断 | 概要 |
| ①連が現れるとき | 【連】とは点が中心線をはさんで上・下側どちらか片側に連続して現れる状態
7点以上 |
| ②周期的な波形を示すとき | ー |
| ③点が連続して上昇または下降の傾向を示すとき | 7点以上 |
| ④点が中心線(CL)に近接して現れるとき | 打点が連続して中心線に近接して現れるときは、異常があるとみて原因を調査する
CLに近接したという判断は、CLを中心として上下の限界線幅の1/2以内の範囲であること |
| ⑤点が管理限界線に近接して現れるとき | 管理限界線とCL幅の1/3まで限界線側に接した場合を異常とみなす
①連続3点のうち2点 ②連続7点のうち3点 ③連続10点のうち5点 |
管理図の種類の覚え方&見方!例題で係数表の使い方まとめ
管理図の種類
| 計数値の管理図(離散的な値) | P管理図 | 不良率の管理図
不適合率を用いて工程を評価する |
| nP管理図 | 不良個数の管理図
不適合数を用いて工程を評価する |
|
| c管理図 | 欠点数の管理図
サンプルの不適合数を用いて工程を評価する |
|
| u管理図 | 単位当たり欠点数の管理図
サンプルの単位当たりの不適合数を用いて工程を評価する |
|
| 計量値の管理図(連続的な値) |
個々の測定値を用いて工程を管理する
一点管理図ともいう |
|
| 群の平均値と範囲を用いて、工程の分散を評価する | ||
| 個々の測定値と範囲、試験誤差を用いて工程を評価する | ||
| メディアンを用いて群間のちがいを評価する |
管理図の覚え方!以下の表をがんばって暗記しよう(記号の定義も)
| 管理図の種類 | 管理図計算式 | |||
| 定義 | 中心線(CL) | 上方管理限界線(UCL) | 下方管理限界線(LCL) | |
| X管理図 | 各試験データの平均 | 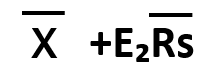 |
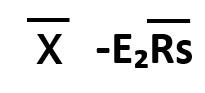 |
|
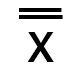 |
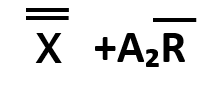 |
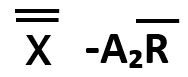 |
||
| R管理図 | 各組R(範囲:最大値と最小値の差)の平均 |  |
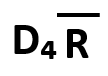 |
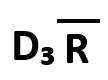 |
| Rs管理図 | データの移動誤差(相となり合ったデータ差の絶対値) | 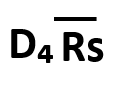 |
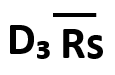
=考えない |
|
| Rm管理図 | 各組Rm(各組のデータの最大値と最小値の差=範囲) | 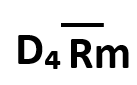 |
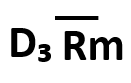 =考えない =考えない |
|
管理図の見方
| 工程が安定していると判断できる基本条件 | 工程が異常なく安定している |
| ①打点がすべて管理限界線のなかに入っている
②点の並び方にクセがない |
①点が連続25点以上管理限界内にある
②連続35点中、限界外に出たものが1点以内 ③連続100点中、限界外に出たものが2点以内 |
| 工程が不安定と判断すべき状態 | 概要 |
| ①連が現れるとき | 【連】とは点が中心線をはさんで上・下側どちらか片側に連続して現れる状態
7点以上 |
| ②周期的な波形を示すとき | ー |
| ③点が連続して上昇または下降の傾向を示すとき | 7点以上 |
| ④点が中心線(CL)に近接して現れるとき | 打点が連続して中心線に近接して現れるときは、異常があるとみて原因を調査する
CLに近接したという判断は、CLを中心として上下の限界線幅の1/2以内の範囲であること |
| ⑤点が管理限界線に近接して現れるとき | 管理限界線とCL幅の1/3まで限界線側に接した場合を異常とみなす
①連続3点のうち2点 ②連続7点のうち3点 ③連続10点のうち5点 |
以上です。
ありがとうございました。
